题目内容
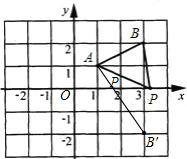
如图,已知点A(1,1)、B(3,2),且P为x轴上一动点,则△ABP的周长的最小值为 .


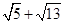 .
.试题分析:本题需先根据已知条件求出AB的长,再根据P为x轴上一动点,确定出P点的位置,即可求出BP+AP的长,最后即可求出△ABP周长的最小值.
试题解析:作点B关于x轴的对称点B′,连接AB′,当点P运动到AB′与X轴的交点时
△ABP周长的最小值.
∵A(1,1),B(3,2),
∴AB=
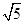
又∵P为x轴上一动点,
当求△ABP周长的最小值时,
∴AB′=
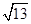
∴△ABP周长的最小值为:AB+AB′=
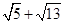

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,并求出三角形
,并求出三角形