题目内容
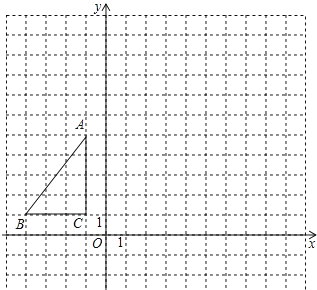
【题目】已知：如图，在△ABC中，∠C=90°，∠A=30°．
（1）用直尺和圆规作AB的垂直平分线，分别交AC、AB于点E．D（保留作图痕迹，不写作法）
（2）猜想AC与CE之间的数量关系，并证明你的猜想．
【答案】（1）作图见解析；（2）
，证明见解析．
【解析】
（1）利用基本作图（作线段的垂直平分线）作DE垂直平分AB；
（2）连接BE，如图，利用线段垂直平分线的性质得EA=EB，则∠A=∠ABE=30°，则可计算出∠CBE=30°，利用含30度的直角三角形三边的关系得到BE=2CE，则AC=3CE．
解：（1）
即为所作
的垂直平分线．
（2）AC=3CE．理由如下：
连接BE，如图，
∵ED垂直平分AB，
∴EA=EB，
∴∠A=∠ABE=30°，
∵∠ABC=60°，
∴∠CBE=30°，
∴BE=2CE，
∴AE=2CE，
∴AC=3CE．
练习册系列答案
相关题目
