题目内容
【题目】等腰直角△ABC中,BC=AC,∠ACB=90°,将该三角形在直角坐标系中放置.

(1)如图(1),过点A作AD⊥x轴,当B点为(0,1),C点为(3,0)时,求OD的长;
(2)如图(2),将斜边顶点A、B分别落在y轴上、x轴上,若A点为(0,1),B点为(4,0),求C点坐标;
【答案】(1)4;(2)(![]() )
)
【解析】
(1)通过证明△BOC≌△CDA,可得CD=OB=1,即可求OD的长;
(2)过点C作CF⊥y轴,CE⊥x轴,通过证明△ACF≌△BCE,可得BE=AF,CF=CE,可证四边形CEOF是正方形,可得CF=OE=OF=CE,即可求点C坐标.
解:(1)∵B点为(0,1),C点为(3,0)
∴OB=1,OC=3
∵∠ACB=90°,
∴∠BCO+∠ACD=90°,且∠BCO+∠OBC=90°
∴∠ACD=∠OBC,且AC=BC,∠BOC=∠ADC=90°,
∴△BOC≌△CDA(AAS)
∴CD=OB=1
∴OD=OC+CD=4
(2)如图,过点C作CF⊥y轴,CE⊥x轴,
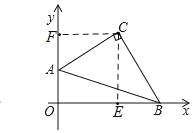
∵A点为(0,1),B点为(4,0),
∴AO=1,BO=4
∵CF⊥y轴,CE⊥x轴,∠AOB=90°,
∴四边形CEOF是矩形,
∴∠ECF=90°,
∴∠FCA+∠ACE=90°,且∠ACE+∠BCE=90°,
∴∠FCA=∠BCE,且AC=BC,∠CFA=∠CEB=90°,
∴△ACF≌△BCE(AAS)
∴BE=AF,CF=CE,
∴矩形CEOF是正方形
∴CF=OE=OF=CE,
∴OA+AF=OB﹣BE
∴2AF=OB﹣OA
∴AF=![]()
∴OF=![]()
∴点C(![]() ,
,![]() )
)

 名校课堂系列答案
名校课堂系列答案【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下(单位:分):
A班:88,91,92,93,93,93,94,98,98,100
B班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
A班 | 100 | a | 93 | 93 | c |
B班 | 99 | 95 | b | 93 | 8.4 |
(1)求表中a、b、c的值;
(2)依据数据分析表,有人说:“最高分在A班,A班的成绩比B班好”,但也有人说B班的成绩要好,请给出两条支持B班成绩好的理由;







