题目内容
如图,在等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,下列结论不一定正确的是( )
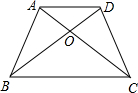
| A.AC=BD | B.OB=OC | C.∠BCD=∠BDC | D.∠ABD=∠ACD |

A、∵四边形ABCD是等腰梯形,
∴AC=BD,
故本选项正确;
B、∵四边形ABCD是等腰梯形,
∴AB=DC,∠ABC=∠DCB,
在△ABC和△DCB中,
∵
DCB,
∴△ABC≌△DCB(SAS),
∴∠ACB=∠DBC,
∴OB=OC,
故本选项正确;
C、∵无法判定BC=BD,
∴∠BCD与∠BDC不一定相等,
故本选项错误;
D、∵∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABD=∠ACD.
故本选项正确.
故选C.
∴AC=BD,
故本选项正确;
B、∵四边形ABCD是等腰梯形,
∴AB=DC,∠ABC=∠DCB,
在△ABC和△DCB中,
∵
|
∴△ABC≌△DCB(SAS),
∴∠ACB=∠DBC,
∴OB=OC,
故本选项正确;
C、∵无法判定BC=BD,
∴∠BCD与∠BDC不一定相等,
故本选项错误;
D、∵∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABD=∠ACD.
故本选项正确.
故选C.

练习册系列答案
相关题目




