题目内容
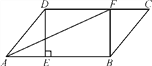
【题目】如图,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
【答案】见解析
【解析】分析:(1)由平行四边形的性质和已知条件得出BE=DF,证明四边形BFDE为平行四边形,再由DE⊥AB,即可得出结论;
(2)由矩形的性质和勾股定理求出BC,得出AD=BC=DF,证出∠DAF=∠DFA,再由平行线的性质即可得出结论.
详解:证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵CF=AE,
∴BE=DF.∴四边形BFDE为平行四边形.
∵DE⊥AB,
∴∠DEB=90°
.∴四边形BFDE是矩形.
(2)∵四边形BFDE是矩形,
∴∠BFD=90°.
∴∠BFC=90°
.在Rt△BFC中,由勾股定理得BC=![]() =10.
=10.
∴AD=BC=10.
又∵DF=10,
∴AD=DF
.∴∠DAF=∠DFA.
∵AB∥CD,
∴∠DFA=∠FAB.
∴∠DAF=∠FAB.
∴AF是∠DAB的平分线.

练习册系列答案
相关题目
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?