题目内容
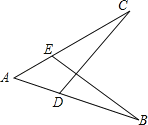
【题目】如图，在△ABC中，AB=BC，∠ACB=90°，点D、E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A、B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C、B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是（ ）
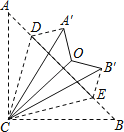
A．90° B．120° C．135° D．150°
【答案】B
【解析】
试题分析：如图所示，延长CO到F，由翻折的性质可知：∠A′CF=
，
，∠CA′O=∠DA′O=∠A=45°，∠OB′C=∠CB′E=∠ECB=45°，最后利用三角形外角的性质可求得∠A′OB′的度数．
解：如图所示：延长CO到F．
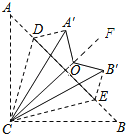
∵AB=BC，∠ACB=90°，
∴∠A=∠B=45°．
由翻折的性质可知：∠A′CF=
，
，∠CA′O=∠DA′O=∠A=45°，∠OB′C=∠CB′E=∠ECB=45°．
∴∠A′CB′=∠A′CF+∠B′CF=
=30°．
∴∠A′OB′=∠A′CB′+∠CA′O+∠OB′C=30°+45°+45°=120°．
故选：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
