题目内容
【题目】如图,AB是⊙O的直径,点C是![]() 的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且
的中点,连接AC并延长至点D,使CD=AC,点E是OB上一点,且![]() ,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.
,CE的延长线交DB的延长线于点F,AF交⊙O于点H,连接BH.

(1)求证:BD是⊙O的切线;(2)当OB=2时,求BH的长.
【答案】(1)证明见解析;(2)BH=![]() .
.
【解析】
(1)先判断出∠AOC=90°,再判断出OC∥BD,即可得出结论;
(2)先利用相似三角形求出BF,进而利用勾股定理求出AF,最后利用面积即可得出结论.
(1)连接OC,
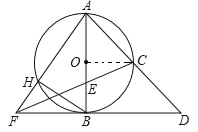
∵AB是⊙O的直径,点C是![]() 的中点,
的中点,
∴∠AOC=90°,
∵OA=OB,CD=AC,
∴OC是△ABD是中位线,
∴OC∥BD,
∴∠ABD=∠AOC=90°,
∴AB⊥BD,
∵点B在⊙O上,
∴BD是⊙O的切线;
(2)由(1)知,OC∥BD,
∴△OCE∽△BFE,
∴![]() ,
,
∵OB=2,
∴OC=OB=2,AB=4,![]() ,
,
∴![]() ,
,
∴BF=3,
在Rt△ABF中,∠ABF=90°,根据勾股定理得,AF=5,
∵S△ABF=![]() ABBF=
ABBF=![]() AFBH,
AFBH,
∴ABBF=AFBH,
∴4×3=5BH,
∴BH=![]() .
.

练习册系列答案
相关题目
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.