题目内容
如图，Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A在
轴上，点B在
轴上，
，∠BAO=
．将Rt△AOB折叠，使BO边落在BA边上，点O与点D重合，折痕为BC．
(1)求直线BC的解析表达式；
(2)求经过B、C、A三点的抛物线
的解析表达式；若抛物线的顶点为M，试判断点M是否在直线BC上，并说明理由
解：(1)∵
∴在Rt△COB中．
）
∴点C的坐标为(1，0)
又点B的坐标为（0，
）
∴设直线BC的解析表达式为：
，
∴
∴
则直线BC的解析表达式为：
（2）∵Rt△AOB中，
∴A(3，0)，
又
,C(1,0)
∴
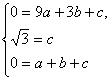
解之得：
，
，
。所求抛物线的解析表达式为
配方得：
，∴顶点为
．
把x=2代入,得
∴顶点M不在直线BC上
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
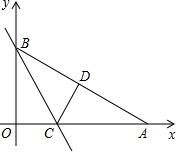如图，Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片，点O与原点重合，点A在x轴上，点B在y轴上，OB=
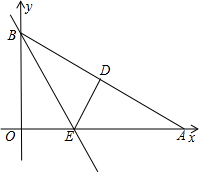痕为BE．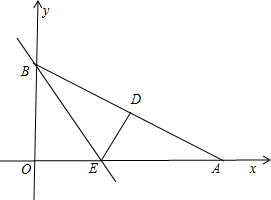
重合，点A在x轴上，点B在y轴上
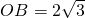，∠OAB=30°，将Rt△AOB折叠，使OB边落在AB边上，点O与点D重合，折
痕为BE．
，∠BAO=30度，将Rt△AOB折叠，使BO边落在BA边上，点O与点D重合，折痕为BC。