题目内容
如图,Rt△AOB是一张放在平面直角坐标系中的三角形纸片,点O与原点重合,点A在x轴正半轴上,点B在y轴正半轴上,OB=2| 3 |
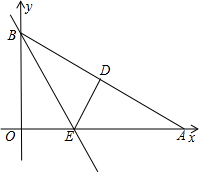 痕为BE.
痕为BE.(1)求点E和点D的坐标;
(2)求经过O、D、A三点的二次函数图象的解析式.
分析:(1)过点D作DF⊥OA,垂足为F,由图形折叠的性质可知△BOE≌△BDE,在直角三角形OAB中,OB=2
,∠OAB=30°,根据锐角三角函数的定义可计算出A,B两点的坐标,根据三角形全等及三角形内角与外角的关系可知∠BEO=60°,BD=
AB,再根据锐角三角函数的定义及三角形中位线定理即可求出D、E两点的坐标.
(2)由(1)可知A、D两点的坐标,O为原点,根据此特点设出二次函数的解析式,把A、D两点分别代入即可求出未知数的值,进而求出其解析式.
| 3 |
| 1 |
| 2 |
(2)由(1)可知A、D两点的坐标,O为原点,根据此特点设出二次函数的解析式,把A、D两点分别代入即可求出未知数的值,进而求出其解析式.
解答: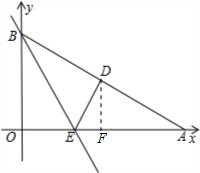 解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合,
解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合,
所以,∠OBE=∠DBE,OB=DB(1分).
由Rt△AOB中,∠OAB=30°,
得∠ABO=60°,
且OA=OBcot30°=6,
得点A(6,0)(1分).
在Rt△AOB中,由∠OBE=30°,得OE=2,得点E(2,0)(1分);
Rt△AOB中,由∠OAB=30°得AB=2OB=2DB,
所以D是AB的中点,
得DF=
OB=
,OF=
OA=3,
得点D(3,
)(2分).
(2)设经过O、D、A三点的二次函数图象的解析式为y=ax2+bx.
把A(6,0),D(3,
))入y=ax2+bx,
得
.(2分)
解得
.(2分)
所以,经过O、D、A三点的二次函数图象的解析式为y=
x2+
x(1分).
 解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合,
解:(1)过点D作DF⊥OA,垂足为F,因为Rt△AOB沿BE折叠时,OB边落在AB边上,点O与点D重合,所以,∠OBE=∠DBE,OB=DB(1分).
由Rt△AOB中,∠OAB=30°,
得∠ABO=60°,
且OA=OBcot30°=6,
得点A(6,0)(1分).
在Rt△AOB中,由∠OBE=30°,得OE=2,得点E(2,0)(1分);
Rt△AOB中,由∠OAB=30°得AB=2OB=2DB,
所以D是AB的中点,
得DF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
得点D(3,
| 3 |
(2)设经过O、D、A三点的二次函数图象的解析式为y=ax2+bx.
把A(6,0),D(3,
| 3 |
得
|
解得
|
所以,经过O、D、A三点的二次函数图象的解析式为y=
-
| ||
| 9 |
2
| ||
| 3 |
点评:本题综合考查了图形折叠及直角三角形的性质,二次函数图象上点的坐标特点,难度不大,但有一定的综合性,是一道好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
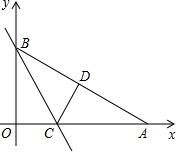 如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=
如图,Rt△AOB是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点B在y轴上,OB=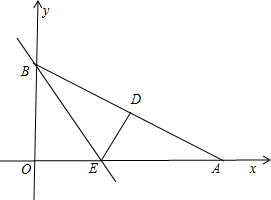 重合,点A在x轴上,点B在y轴上
重合,点A在x轴上,点B在y轴上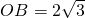 ,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折
,∠OAB=30°,将Rt△AOB折叠,使OB边落在AB边上,点O与点D重合,折 痕为BE.
痕为BE. ,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。
,∠BAO=30度,将Rt△AOB折叠,使BO边落在BA边上,点O与点D重合,折痕为BC。