题目内容
【题目】如图,已知正方形 ABCD 的边长为 10,E 在 BC 边上运动,取 DE 的中点 G,EG 绕点 E 顺时针旋转90°得 EF,问 CE 长为多少时,A、C、F 三点在一条直线上( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
过F作BC的垂线,交BC延长线于N点,连接AF.只要证明Rt△FNE∽Rt△ECD,利用相似比2:1解决问题.再证明△CNF是等腰直角三角形即可解决问题.
过F作BC的垂线,交BC延长线于N点,连接AF.
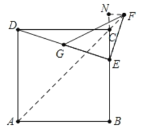
∵∠DCE=∠ENF=90°,∠DEC+∠NEF=90°,∠NEF+∠EFN=90°,
∴∠DEC=∠EFN,
∴Rt△FNE∽Rt△ECD,
∵DE的中点G,EG绕E顺时针旋转90°得EF,
∴两三角形相似比为1:2,
∴可以得到CE=2NF,NE=![]() CD=5.
CD=5.
∵AC平分正方形直角,
∴∠NFC=45°,
∴△CNF是等腰直角三角形,
∴CN=NF,
∴CE=![]() NE=
NE=![]() 5=
5=![]() ,
,
故选C.

【题目】经测算,某地气温![]() 与距离地面的高度
与距离地面的高度![]() 有如下对应关系:
有如下对应关系:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 26 | 20 | 14 | 8 |
| -4 | … |
请根据上表,完成下面的问题.
(1)猜想:距离地面的高度每上升![]() ,气温就下降______
,气温就下降______![]() ;表中
;表中![]() ______.
______.
(2)气温![]() 与高度
与高度![]() 之间的函数关系式是______.
之间的函数关系式是______.
(3)求该地距离地面![]() 处的气温.
处的气温.
【题目】抗震救灾中,某县粮食局为了保证库存粮食的安全,决定将甲、乙两个仓库的粮食,全部转移到具有较强抗震功能的A、B两仓库.已知甲库有粮食100吨,乙库有粮食80吨,而A库的容量为70吨,B库的容量为110吨.从甲、乙两库到A、B两库的路程和运费如下表:(表中“元/吨千米”表示每吨粮食运送1千米所需人民币)
路程(千米) | 运费(元/吨千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
(1)若甲库运往A库粮食x吨,请写出将粮食运往A、B两库的总运费y(元)与x(吨)的函数关系式;
(2)当甲、乙两库各运往A、B两库多少吨粮食时,总运费最省,最省的总运费是多少?