题目内容
【题目】在等腰
中，
,
为
边上的高，点
在的外部且
，
,连接
交直线于点
，连接
．
(1)如图①，当
时，求证：
；
(2)如图②，当
时，求
的度数；
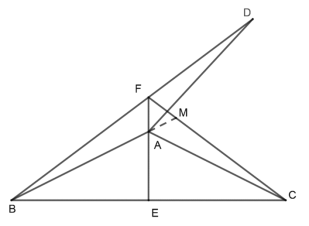
(3)如图③，当
时,求证：
．
【答案】（1）见解析；（2）
；（3）见解析
【解析】
（1）根据等腰三角形三线合一的性质，可得AE垂直平分BC，F为垂直平分线AE上点，即可得出结论；
（2）根据（1）的结论可得AE平分∠BAC，∠BAF=20°，由AB=AC=AD，推出
，根据外角性质可得
计算即可；
（3）在CF上截取CM=DF，连接AM，证明△ACM≌△ADF（SAS），进而证得△AFM为等边三角形即可．
（1）证明：∵AE为等腰△ABC底边BC上的高线，AB=AC，
，∠AEB=∠AEC=90°，BE=CE，
∴AE垂直平分BE，F在AE上，
；
(2) 
，
，
，
，
由（1）知，AE平分∠BAC，
，
，
故答案为：60°；
(3) 在CF上截取CM=DF，连接AM，
由（1）可知，∠ABC=∠ACB，∠ABE=∠ACE，
，
，
，
，
在△ACM和△ADF中，
∴△ACM≌△ADF（SAS），
，
，
∴△AFM为等边三角形，
，
．
练习册系列答案
相关题目
【题目】中华文明，源远流长；中华汉字，寓意深广，为传承中华优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写大赛”
为了解本次大赛的成绩，校团委随机抽取了其中若干名学生的成绩作为样本进行统计，制成如下不完整的统计图表：
成绩 | 频数 | 频率 |
| 10 |
|
| 30 |
|
| 40 | n |
| m |
|
| 50 |
|
a | 1 |
请根据所给信息，解答下列问题：
______，
______，
______；
补全频数直方图；
这若干名学生成绩的中位数会落在______分数段；
若成绩在90分以上
包括90分
的为“优”等，请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人？
