题目内容
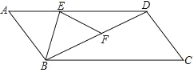
【题目】如图,在△ABC中,∠BAC=50°.
(1)若点I是∠ABC,∠ACB的角平分线的交点,则∠BIC= °.
(2)若点D是∠ABC,∠ACB的外角平分线的交点,则∠BDC= °.
(3)若点E是∠ABC,∠ACG的平分线的交点,探索∠BEC与∠BAC的数量关系,并说明理由.
(4)在(3)的条件下,若CE∥AB,求∠ACB的度数.

【答案】(1)115°;(2)65°;(3)∠BEC =![]() ∠BAC,理由见解析;(4)80°.
∠BAC,理由见解析;(4)80°.
【解析】
(1)根据三角形的内角和定理以及角平分线的定义进行计算;
(2)根据三角形的内角和定理、角平分线的定义以及外角的性质进行计算即可;
(3)根据三角形的内角和定理、角平分线的定义以及外角的性质进行计算即可得出结论;
(4)根据平行线的性质以及邻补角的定义进行计算即可.
(1)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∵点I是∠ABC,∠ACB的角平分线的交点,
∴∠IBC+∠ICB=65°,
∴△IBC中,∠BIC=180°-65°=115°;
(2)∵△ABC中,∠BAC=50°,
∴∠ABC+∠ACB=130°,
∴∠ABC,∠ACB的外角之和=360°-130°=230°,
∵点D是∠ABC,∠ACB的外角平分线的交点,
∴∠DBC+∠DCB=115°,
∴△DBC中,∠BDC=180°-115°=65°;
(3)∠BEC=![]() ∠BAC.
∠BAC.
∵∠DCE是△BCE的外角,
∴∠E=∠DCE-∠CBE,
∵点E是∠ABC,∠ACG的平分线的交点,
∴∠DCE=![]() ∠ACD,∠CBE=
∠ACD,∠CBE=![]() ∠ABC,
∠ABC,
∴∠E=![]() ∠ACD-
∠ACD-![]() ∠ABC=
∠ABC=![]() (∠ACD-∠ABC)=
(∠ACD-∠ABC)=![]() ∠A,
∠A,
即∠BEC=![]() ∠BAC;
∠BAC;
(4)∵CE∥AB,
∴∠A=∠ACE=50°,
∵CE平分∠ACD,
∴∠ACD=100°,
∴∠ACB=180°-100=80°.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案