题目内容
【题目】如图，在△OAB中， CD∥AB，若OC:OA =1:2，则下列结论：（1）
；（2）；（3）
. 其中正确的结论是（ ）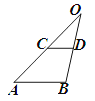
A.（1）（2）
B.（1）（3）
C.（2）（3）
D.（1）（2）（3）
【答案】A
【解析】在三角形的证两边的关系大小，与面积关系中常常可利用全等或，相似三角形证得。本题中属于相似三角形的类型，∵在△OAB中， CD∥AB，∴△OAB∽△OCD ∴
,又∵OC:OA =1:2∴AB =2 CD。因为两个三角形相似，那么相似比的平方等于面积比，所以，选项（3)错误，（1)（2)正确。
选A
【考点精析】关于本题考查的平行线分线段成比例和相似三角形的判定与性质，需要了解三条平行线截两条直线，所得的对应线段成比例；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．
练习册系列答案
阅读快车系列答案
相关题目