题目内容
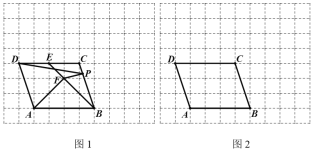
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,连接
,连接![]() 、
、![]() 交于点
交于点![]() .
.
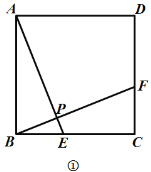
(1)如图①,判断![]() 和
和![]() 之间的数量关系和位置关系,并证明;
之间的数量关系和位置关系,并证明;
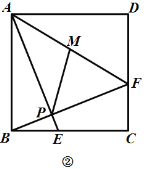
(2)如图②,连接![]() ,点
,点![]() 是
是![]() 中点,若
中点,若![]() ,
,![]() ,求线段
,求线段![]() 的长度;
的长度;
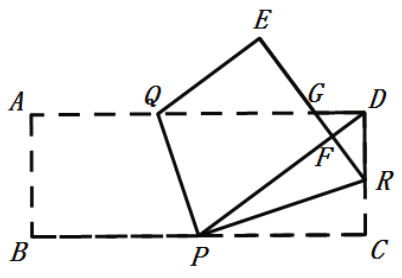
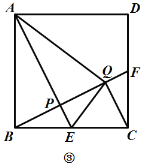
(3)如图③,作![]() 于点
于点![]() ,若
,若![]() ,求证:点
,求证:点![]() 是
是![]() 中点.
中点.
【答案】(1)![]() ,
,![]() ,证明见解析;(2)
,证明见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先根据正方形的性质可得![]() ,
,![]() ,再根据三角形全等的判定定理与性质可得
,再根据三角形全等的判定定理与性质可得![]() ,
,![]() ,然后根据等量代换、三角形的内角和定理可得
,然后根据等量代换、三角形的内角和定理可得![]() ,由此即可得
,由此即可得![]() ;
;
(2)先根据三角形全等的性质、正方形的性质求出![]() ,再根据勾股定理可求出
,再根据勾股定理可求出![]() ,然后结论(1)的结论,利用直角三角形的性质即可得;
,然后结论(1)的结论,利用直角三角形的性质即可得;
(3)先根据相似三角形的判定与性质得出![]() ,再根据相似三角形的性质可得
,再根据相似三角形的性质可得![]() ,从而可得
,从而可得![]() ,即可得出
,即可得出![]() ,然后由(1)已证出
,然后由(1)已证出![]() ,最后根据等量代换可得
,最后根据等量代换可得![]() ,即得证.
,即得证.
(1)![]() ,
,![]() ,证明如下:
,证明如下:
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
(2)由(1)已证:![]()
![]()
∵![]() ,
,![]()
![]()
∵四边形![]() 是正方形
是正方形
![]()
∴![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:![]()
由(1)已证:![]()
![]() 是直角三角形
是直角三角形
在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 中点
中点
∴![]() ;
;
(3)∵![]()
∴![]()
又![]()
∴![]()
∴![]()
∵![]()
∴![]() ,即
,即![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴点![]() 是
是![]() 中点.
中点.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】下表中给出![]() ,
,![]() ,
,![]() 三种手机通话的收费方式.
三种手机通话的收费方式.
收费方式 | 月通话费/元 | 包时通话时间/ | 超时费/(元/ |
|
|
|
|
|
|
|
|
|
| 不限时 |
(1)设月通话时间为![]() 小时,则方案
小时,则方案![]() ,
,![]() ,
,![]() 的收费金额
的收费金额![]() ,
,![]() ,
,![]() 都是
都是![]() 的函数,请分别求出这三个函数解析式.
的函数,请分别求出这三个函数解析式.
(2)填空:
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
若选择方式![]() 最省钱,则月通话时间
最省钱,则月通话时间![]() 的取值范围为______;
的取值范围为______;
(3)小王、小张今年![]() 月份通话费均为
月份通话费均为![]() 元,但小王比小张通话时间长,求小王该月的通话时间.
元,但小王比小张通话时间长,求小王该月的通话时间.
【题目】某校为了调查学生对卫生健康知识,特别是疫情防控下的卫生常识的了解,现从九年级![]() 名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
组别 | 成绩 | 人数 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|

请结合图表信息完成下列各题.
(1)表中a的值为_____,b的值为______;在扇形统计图中,第![]() 组所在扇形的圆心角度数为______°;
组所在扇形的圆心角度数为______°;
(2)若测试成绩不低于![]() 分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
(3)若测试成绩在![]() 分以上(含
分以上(含![]() 分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.