Question

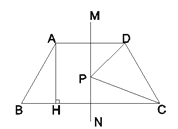
【题目】如图，题型ABCD中，AD∥BC，AD=CD=AD=2，∠B=60°，AH⊥BC于点H，且AH=，直线MN是梯形的对称轴，P为直线MN上的一动点，则PC＋PD的最小值为______.

Answer 1

【答案】

【解析】试题解析：连接AC交直线MN于P点，P点即为所求．

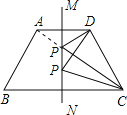
∵直线MN为梯形ABCD的对称轴，
∴AP=DP，
∴当A、P、C三点位于一条直线时，PC+PD=AC，为最小值，
∵AD=DC=AB，AD∥BC，
∴∠DCB=∠B=60°，
∵AD∥BC，
∴∠ACB=∠DAC，
∵AD=CD，
∴∠DAC=∠DCA，
∴∠DAC=∠DCA=∠ACB
∵∠ACB+∠DCA=60°，
∴∠DAC=∠DCA=∠ACB=30°，
∴∠BAC=90°，
∵AB=2，∠B=60°
∴AC=tan60°×AB=×2=2．
∴PC+PD的最小值为2．