题目内容
如图,直线l:y=x+1与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数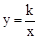 的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.

(1)求反比例函数的解析式;
(2)求AN•BM的值.
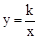 的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
的图象经过点C,点P在反比例函数图象上且位于C点左侧,过点P作x轴、y轴的垂线分别交直线l于M、N两点.
(1)求反比例函数的解析式;
(2)求AN•BM的值.
解:(1)连接AC,BC,由题意得:四边形AOBC为正方形,
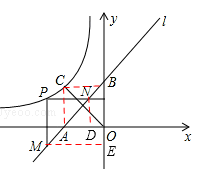
对于一次函数y=x+1,令x=0,求得:y=1;
令y=0,求得:x=﹣1。
∴OA=OB=1。∴C(﹣1,1)。
将C(﹣1,1)代入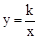 得:
得: ,即k=﹣1。
,即k=﹣1。
∴反比例函数解析式为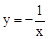 。
。
(2)过M作ME⊥y轴,作ND⊥x轴,
设P(a,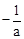 ),可得ND=
),可得ND=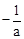 ,ME=|a|=﹣a,
,ME=|a|=﹣a,
∵△AND和△BME为等腰直角三角形,
∴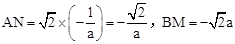 。
。
∴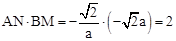 。
。

对于一次函数y=x+1,令x=0,求得:y=1;
令y=0,求得:x=﹣1。
∴OA=OB=1。∴C(﹣1,1)。
将C(﹣1,1)代入
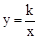 得:
得: ,即k=﹣1。
,即k=﹣1。∴反比例函数解析式为
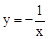 。
。(2)过M作ME⊥y轴,作ND⊥x轴,
设P(a,
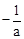 ),可得ND=
),可得ND=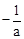 ,ME=|a|=﹣a,
,ME=|a|=﹣a,∵△AND和△BME为等腰直角三角形,
∴
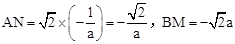 。
。∴
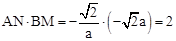 。
。试题分析:(1)连接AC,BC,由题意得:四边形AOBC为正方形,对于一次函数解析式,分别令x与y为0求出对于y与x的值,确定出OA与OB的值,进而C的坐标,代入反比例解析式求出k的值,即可确定出反比例解析式。
(2)过M作ME⊥y轴,作ND⊥x轴,根据P在反比例解析式上,设出P坐标得出ND的长,根据三角形AND为等腰直角三角形表示出AN与BM的长,即可求出所求式子的值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线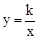 在第一象限内交于点B,BC丄x轴于点C,OC=2AO.求双曲线的解析式.
在第一象限内交于点B,BC丄x轴于点C,OC=2AO.求双曲线的解析式.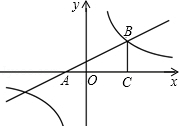
 的图象经过(1,2),则反比例函数
的图象经过(1,2),则反比例函数 的图象经过点(2, ).
的图象经过点(2, ). 与反比例函数
与反比例函数 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将
 ,求反比例函数的解析式.
,求反比例函数的解析式. 上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是
上,点P、Q分别是x轴、y轴上的动点,当四边形PABQ的周长取最小值时,PQ所在直线的解析式是
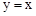

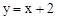
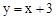
 的图象的一个交点为A(1,m) .过点B作AB的垂线BD,与反比例函数
的图象的一个交点为A(1,m) .过点B作AB的垂线BD,与反比例函数 (x>0)的图象交于点D(n,-2).
(x>0)的图象交于点D(n,-2).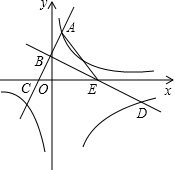
 的图象上,则y1、y2、y3的大小关系是
的图象上,则y1、y2、y3的大小关系是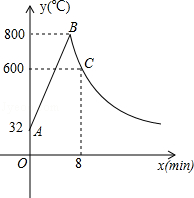
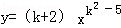 是y关于x的反比例函数,则k= .
是y关于x的反比例函数,则k= .