题目内容
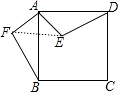
【题目】如图,点E是正方形ABCD内的一点,将△ADE绕点A顺时针旋转90°至△ABF.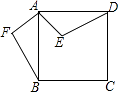
(1)直接写出图中一组相等的线段和一组相等的角.
(2)若∠ADE=35°,∠DAE=50°,求∠F的度数.
(3)若连接EF,则△AEF是三角形.
【答案】
(1)解:由旋转不变性可知:AE=AF,∠ADE=∠ABF
(2)解:∵∠EAD+∠ADE+∠E=180°,∠ADE=35°,∠DAE=50°,
∴∠E=180°﹣35°﹣50°=95°,
由旋转不变性可知:∠F=∠E=95°
(3)等腰直角
【解析】解: (1)由旋转不变性可知:AE=AF,∠ADE=∠ABF;
(2)∵∠EAD+∠ADE+∠E=180°,∠ADE=35°,∠DAE=50°,
∴∠E=180°﹣35°﹣50°=95°.
由旋转不变性可知:∠F=∠E=95°;
(3)连接EF.
∵AF=AE,∠EAF=90°,
∴△AEF是等腰直角三角形,
所以答案是:(1)AE=AF,∠ADE=∠ABF;(2)∠F=95°;(3)等腰直角.
【考点精析】认真审题,首先需要了解正方形的性质(正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形),还要掌握旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了)的相关知识才是答题的关键.

练习册系列答案
相关题目