题目内容
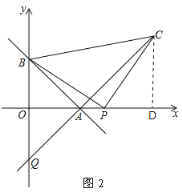
【题目】已知,如图,一次函数![]() 与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.
与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°.

(1)求一次函数的表达式;
(2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q.
①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式;
②当P点在x轴正半轴运动时,Q点的位置是否发现变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围.
【答案】(1)![]() ;(2)①点C(7,4);
;(2)①点C(7,4);![]() ;②点Q的位置不发生变化,点Q的坐标为(0,-3).
;②点Q的位置不发生变化,点Q的坐标为(0,-3).
【解析】
试题(1)由∠AOB=90°,∠OAB=45°,可得∠OBA=∠OAB=45°,即OA=OB,由A(3,0),可得B(0,3),代入y=kx+b可得出k,b的值,即可得出一次函数的表达式;
(2)①过点C作x轴的垂线,垂足为D,易证△BOP≌△PDC,进而得出点P,C的坐标,把点A,C的坐标代入y=k1x+b1求解即可;
②由△BOP≌△PDC,可得PD=BO,CD=PO,由线段关系进而得出OA=OB,得出AD=CD,由角的关系可得△AOQ是等腰直角三角形,可得出OQ=OA,即可得出点Q的坐标.
试题解析:解:(1)∵∠AOB=90°,∠OAB=45°,
∴∠OBA=∠OAB=45°,
∴OA=OB,
∵A(3,0),
∴B(0,3),
∴![]() ,解得
,解得![]() ,
,
∴![]() ;
;
(2)①过点C作x轴的垂线,垂足为D,
∵∠BPO+∠CPD=∠PCD+∠CPD=90°,
∴∠BPO=∠PCD,
在△BOP和 △PDC 中,
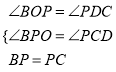 ,
,
∴ △BOP≌ △PDC(AAS).
∴PD=BO=3,CD=PO,
∵P(4,0),
∴CD="PO=4," 则OD=3+4=7,
∴ 点C(7,4),
设直线AC的函数关系式为![]() ,
,
则![]() ,解得
,解得![]() ,
,
∴直线AC的函数关系式为![]() ;
;
②点Q的位置不发生变化.
理由:由①知 △BOP≌ △PDC,
当P点在x轴正半轴运动时,仍有△BOP≌ △PDC,
∴PD=BO,CD=PO,
∴PO+PD=CD+OB,
即OA+AD=OB+CD,
又∵OA=OB,
∴AD=CD,
∴∠CAD=45°,
∴∠CAD=∠QAO=45°,
∴OQ=OA=3,
即点Q的坐标为(0,-3).