题目内容
李倩同学在学习中善于总结解决问题的方法,并把总结出的结果灵活运用到做题中.例如,总结出“图形中有角平分线+平行线,通常会出现等腰三角形”后,老师出了这样一道题:
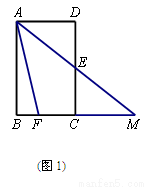
(1)如图1,在矩形ABCD中,F是BC边上的一点,AE平分∠FAD,与CD交于点E,与BC的延长线交于点M,E是CD的中点,请问 AF=FC+AD成立吗?
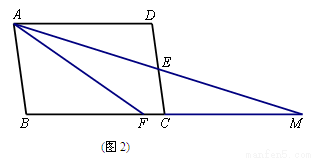
(2)若把矩形ABCD变成平行四边形ABCD(如图2),其它条件不变,你的结论还正确吗?说明理由.
(1) AF=FC+AD成立.
(2) AF=FC+AD成立 ;理由见解析
【解析】
试题分析:(1)由E为CD中点,AD//BM这些条件利用AAS可得△ADE≌△MCE,从而得AD=CM,再由AE平分∠FAD、AD//BM可得AF=FM,从而可得;
(2)由E为CD中点,AD//BM这些条件利用AAS可得△ADE≌△MCE,从而得AD=CM,再由AE平分∠FAD、AD//BM可得AF=FM,从而可得.
试题解析:(1) AF=FC+AD成立.
(2) AF=FC+AD成立
理由:在□ABCD中
∵AD∥BC,
∴∠DAE=∠M.
∵AE平分∠FAD,
∴∠DAE=∠FAM.
∴∠M=∠FAM.
∴AF=FM
∵E是CD的中点,
∴DE=CE
在△ADE和△MCE中,
 ,
,
∴△ADE≌△MCE(AAS).
∴AD=CM .
∵AF=FM=FC+CM,
∴AF=FC+AD.
考点:1、平行四边形的性质;2、等腰三角形的判定;3、三角形全等的判定

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目