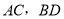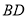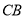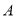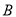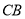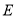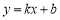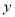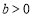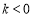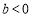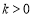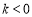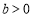题目内容
小明和小亮用图中所示的转盘做游戏:分别转动转盘两次,若两次指针指向的数字之差(第一次数字减第二次的数字)大于或等于2,小明获胜,否则小亮获胜(指针恰好指在等分线上时重新转动转盤).
(1)分别求出小明和小亮得分的概率;
(2)你认为游戏是否公平?若公平,请说明理由.

(1)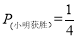 ,
, ;
;
(2)这个游戏规则不公平.
【解析】
试题分析:(1)先根据已知列表,再根据概率公式分别求出小明和小亮得分的概率即可;
(2)根据(1)求出的概率,比较出小明和小亮得分的概率大小,即可判断出是否公平.
试题解析:(1)依题意列表如下:
| 1 | 2 | 3 | 4 |
1 | 0 | 1 | 2 | 3 |
2 | -1 | 0 | 1 | 2 |
3 | -2 | -1 | 0 | 1 |
4 | -3 | -2 | -1 | 0 |
故所有等可能结果有12种,其中数字之差大于等于2的结果有3种,其它结果有9种.
∴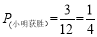 ,
,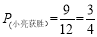 ;
;
(2)这个游戏规则不公平.  ,小亮获胜的概率大.
,小亮获胜的概率大.
考点:1.游戏公平性2.列表法与树状图法.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目