题目内容
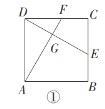
【题目】（1）如图①，在正方形
中，
、
分别是
、
边上的点，
，连接
，
交于点
．求证：
且
；
（2）如图②，若点、分别在
、
的延长线上，且，（1）中的结论是否成立？如果成立，请说明理由；
（3）如图③，在图②的基础上连接
、
、
、
、
、
分别是、、
、
的中点，请直接写出四边形
的形状．
【答案】（1）证明见解析；（2）成立，理由见解析；（3）正方形．
【解析】
（1）首先由正方形的性质判定
，得出
，然后进行等量转换即可得出
；
（2）首先由正方形的性质得出
，判定，得出，然后进行等量转换即可得出；
（3）由中位线定理和（2）中的结论即可判定.
（1）∵四边形
是正方形
∴
∵
∴
即
∴
∴
∴
∵
∴
∴
∴
（2）（1）中的结论成立
∵四边形是正方形
∴
又∵
∴
即
∴
∴
∴
∵
∴
∴
∴
（3）四边形
是正方形
∵
、
、
、
分别是
、
、
、
的中点，
∴
由（2）结论，得，
∴
，∠HMN=∠MNP=∠NPH=∠PHM=90°
∴四边形是正方形
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
【题目】某游泳馆每年夏季推出两种游泳付费方式，方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元．
设小明计划今年夏季游泳次数为x（x为正整数）．
（I）根据题意，填写下表：
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用（元） | 150 | 175 | ______ | … | ______ |
方式二的总费用（元） | 90 | 135 | ______ | … | ______ |
（Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？
（Ⅲ）当x>20时，小明选择哪种付费方式更合算？并说明理由．
