Question

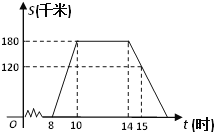
【题目】如图，A是∠MON边OM上一点，AE∥ON．

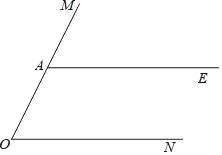
（1）在图中作∠MON的角平分线OB（要求用尺规），交AE于点B；过点A画OB的垂线，垂足为点D，交ON于点C，连接CB，将图形补充完整．

（2）判断四边形OABC的形状，并证明你的结论．

解：四边形OABC是　 　．

Answer 1

【答案】(1)详见解析;(2)四边形OABC是菱形,详见解析

【解析】

（1）根据角平分线的尺规作图即可得；

（2）先证△ADB≌△CDO得AB＝OC，结合AB∥OC知四边形OABC是平行四边形，依据AC⊥OB即可得证．

解：（1）如图所示：

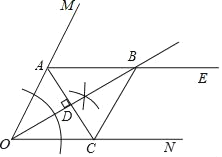
（2）四边形OABC是菱形

证明：∵OB平分∠MON，

∴∠AOB＝∠COB．

∵AE∥ON，

∴∠ABO＝∠COB．

∴∠AOB＝∠ABO．

∴AO＝AB，

∵AC⊥OB，

∴OD＝BD．

在△ADB和△CDO中，

∴△ADB≌△CDO（ASA），

∴AB＝OC．

又∵AB∥OC，

∴四边形OABC是平行四边形，

又∵AC⊥OB，

∴四边形OABC是菱形．