题目内容
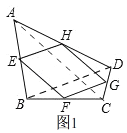
【题目】【再现】如图①，在△ABC中，点D，E分别是AB，AC的中点，可以得到：DE∥BC，且DE=
BC．（不需要证明）
【探究】如图②，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，判断四边形EFGH的形状，并加以证明．
【应用】在（1）【探究】的条件下，四边形ABCD中，满足什么条件时，四边形EFGH是菱形？你添加的条件是： ．（只添加一个条件）
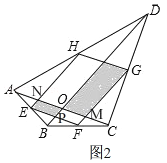
（2）如图③，在四边形ABCD中，点E，F，G，H分别是AB，BC，CD，DA的中点，对角线AC，BD相交于点O．若AO=OC，四边形ABCD面积为5，则阴影部分图形的面积和为 ．
【答案】【探究】平行四边形；【应用】（1）添加AC=BD；（2）
．
【解析】试题分析：【探究】利用三角形的中位线定理可得出HG=EF、EF∥GH，继而可判断出四边形EFGH的形状；
【应用】（1）同【探究】的方法判断出EF=
AC，即可判断出EF=FG，即可得出结论；
（2）先判断出S△BCD=4S△CFG，同理：S△ABD=4S△AEH，进而得出S四边形EFGH=
，再判断出OM=ON，进而得出S阴影=
S四边形EFGH即可．
试题解析：解：【探究】平行四边形．理由：如图1，连接AC，∵E是AB的中点，F是BC的中点，∴EF∥AC，EF=
AC，同理HG∥AC，HG=
AC，综上可得：EF∥HG，EF=HG，故四边形EFGH是平行四边形．
【应用】（1）添加AC=BD．理由：连接AC，BD，同（1）知，EF=
AC，同【探究】的方法得，FG=
BD，∵AC=BD，∴EF=FG，∵四边形EFGH是平行四边形，∴EFGH是菱形；
故答案为：AC=BD；
（2）如图2，由【探究】得，四边形EFGH是平行四边形，∵F，G是BC，CD的中点，∴FG∥BD，FG=
BD，∴△CFG∽△CBD，∴
，∴S△BCD=4S△CFG，同理：S△ABD=4S△AEH，∵四边形ABCD面积为5，∴S△BCD+S△ABD=5，∴S△CFG+S△AEH=
，同理：S△DHG+S△BEF=
，∴S四边形EFGH=S四边形ABCD﹣（S△CFG+S△AEH+S△DHG+S△BEF）=5﹣
=
，设A与FG，EH相交于M，N，EF与BD相交于P，∵FG∥BD，FG=
BD，∴CM=OM=
OC，同理：AN=ON=
OA，∵OA=OC，∴OM=ON，易知，四边形ENOP，FMOP是平行四边形，∴S阴影=
S四边形EFGH=
．故答案为： 
．
