题目内容
(1)已知:如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,且DE=DF.求证:△ABC是等腰三角形.
(2)求证:等腰三角形底边的中点到两腰的距离相等.
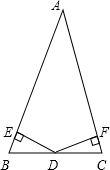
证明:(1)∵D是BC的中点,
∴BD=DC,
∵DE⊥AB,DF⊥AC,
∴△BED和△DFC是Rt△,
又∵DE=DF,
∴△BED≌△DFC,
∴∠B=∠C,
∴△ABC是等腰三角形.
(2)已知:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,
求证:DE=DF.
证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°
∵D是BC的中点,
∴△BED≌△DFC,
∴DE=DF.
分析:(1)根据D是BC的中点和DE⊥AB,DF⊥AC,利用HL求证△BED≌△DFC即可.
(2)根据AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,利用AAS求证△BED≌△DFC即可.
点评:此题主要考查学生对等腰三角形的判定与性质和全等三角形的判定与性质的理解和掌握,证明此题要求学生必须熟练掌握判定全等三角形的几个定理.
∴BD=DC,
∵DE⊥AB,DF⊥AC,
∴△BED和△DFC是Rt△,
又∵DE=DF,
∴△BED≌△DFC,
∴∠B=∠C,
∴△ABC是等腰三角形.
(2)已知:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,
求证:DE=DF.
证明:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°
∵D是BC的中点,
∴△BED≌△DFC,
∴DE=DF.
分析:(1)根据D是BC的中点和DE⊥AB,DF⊥AC,利用HL求证△BED≌△DFC即可.
(2)根据AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,利用AAS求证△BED≌△DFC即可.
点评:此题主要考查学生对等腰三角形的判定与性质和全等三角形的判定与性质的理解和掌握,证明此题要求学生必须熟练掌握判定全等三角形的几个定理.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
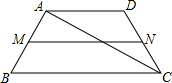 已知:如图,在梯形ABCD中,AD∥BC,AB=DC=8,对角线AC⊥AB,∠B=60°,M、N分别是边AB、DC的中点,连接MN,求线段MN的长.
已知:如图,在梯形ABCD中,AD∥BC,AB=DC=8,对角线AC⊥AB,∠B=60°,M、N分别是边AB、DC的中点,连接MN,求线段MN的长.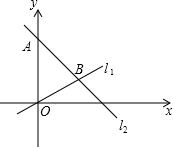 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).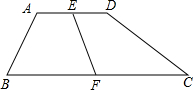 (1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).
(1)在△ABC中,AB=m2-n2,AC=2mn,BCm2+n2=(m>n>0).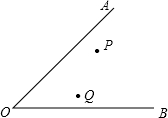 已知:如图,在公路OA、OB的交叉区域有P、Q两所学校,现要在其中建一个图书馆O′使它到两条公路的距离相等,到两所学校的距离也相等,在图中标出图书馆应建的位置O′.
已知:如图,在公路OA、OB的交叉区域有P、Q两所学校,现要在其中建一个图书馆O′使它到两条公路的距离相等,到两所学校的距离也相等,在图中标出图书馆应建的位置O′.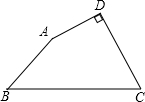 已知:如图,在四边形ABCD中,∠BAD=150°,∠D=90°,AD=2,AB=5,CD=
已知:如图,在四边形ABCD中,∠BAD=150°,∠D=90°,AD=2,AB=5,CD=