题目内容
【题目】折纸中的数学:打开本指书刊幅面的规格大小.如图①,将一张矩形印刷用纸对折后可以得到2开纸,再对折得到4开纸,以此类推可以得到8开纸、16开纸……
若这张矩形印刷用纸的短边长为a.
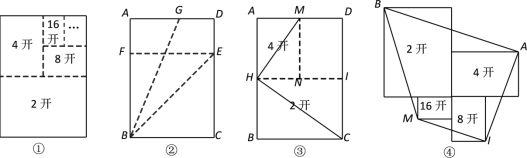
(1)如图②,若将这张矩形印刷用纸ABCD(AB>BC)进行折叠,使得BC与AB重合,点C落在点F处,得到折痕BE;展开后,再次折叠该纸,使点A落在E处,此时折痕恰好经过点B,得到折痕BG,求![]() 的值.
的值.
(2)如图③,②中的矩形纸片ABCD折成2开纸BCIH和4开纸AMNH,它们的对角线分别是HC、HM.说明HC⊥HM.
(3)将图①中的2开纸、4开纸、8开纸和16开纸按如图④所示的方式摆放,依次连接点A、B、M、I,则四边形ABMI的面积是 .(用含a的代数式表示)
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
(1)有折叠的性质,第一次折叠可得BC=CE=a,BE=![]() a,二次折叠
a,二次折叠
AB=BE=![]() a,可得
a,可得![]() 的值;
的值;
(2)由矩形的性质可得△MAH∽△HBC,可得结论.
(3) 由折叠的性质可得答案.
解:(1)∵四边形ABCD是矩形,∴∠ABC=∠C=90°.
∵第一次折叠使点C落在AB上的F处,并使折痕经过点B,
∴∠CBE=∠FBE=45°.
∴∠CBE=∠CEB=45°.
∴BC=CE=a,BE=![]() a.
a.
∵第二次折叠纸片,使点A落在E处,得到折痕BG,
∴AB=BE=![]() a.
a.
∴![]() =
=![]()
(2)根据题意和(1)中的结论,有AH=BH=![]() a,AM=
a,AM=![]() a.
a.
∴![]() =
=![]() =
=![]() .
.
∵四边形ABCD是矩形,
∴∠A=∠B=90°.
∴△MAH∽△HBC.
∴∠AHM=∠BCH.
∵∠BCH+∠BHC=90°.
∴∠AHM+∠BHC=90°.
∴∠MHC=90°.
∴HC⊥HM.
(3)![]() a2.
a2.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目