Question

【题目】周末，小明坐公交车到滨海公园游玩，他从家出发0.8小时候达到中心书城，逗留一段时间后继续坐公交车到滨海公园，小明离家一段时间后，爸爸驾车沿相同的路线前往海滨公园，并比小明早到达，已知爸爸的平均速度是小明从家到中心书城平均速度的两倍.如图是他们离家路程s(km)与小明离家时间t(h)的关系图，请根据图回答下列问题：

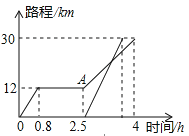
（1）小明家到滨海公园的路程为 km，小明在中心书城逗留的时间为 h；

（2）小明从中心书城到滨海公园的平均速度是 km/h，

（3）小明爸爸比小明早到达多长时间？

（4）爸爸驾车经过多长时间追上小明？

Answer 1

【答案】（1）30；1.7（2）12（3）0.5h（4）h

【解析】

（1）根据横坐标表示时间，纵坐标表示路程，即可得出答案；

（2）根据相应的路程除以时间，即可得出速度；

（3）根据爸爸的平均速度是小明从家到中心书城平均速度的两倍求出爸爸的速度，即可求出爸爸达到的时间，故可求解；

（4）设爸爸驾车经过x小时追上小明，根据路程与速度的关系列出方程即可求解．

（1）小明家到滨海公园的路程为30km，小明在中心书城逗留的时间为2.5-0.8=1.7h，

故答案为：30；1.7；

（2）小明从中心书城到滨海公园的平均速度是km/h，

故答案为：12；

（3）小明从家到中心书城平均速度是12÷0.8=15km/h，

∴小明爸爸前往滨海公园的平均速度是30 km/h，

故小明爸爸到达滨海公园需要的时间为：30÷30=1h，

则在函数图像上表示为2.5+1=3.5h，

∵小明到达海滨公园的时间为4h，

∴小明爸爸比小明早到达4-3.5=0.5h，

（4）设爸爸驾车经过x小时追上小明，

依题意得30x-12x=12，

解得x=，

答：爸爸驾车经过h追上小明．