题目内容
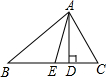
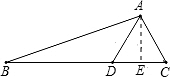
在△ABC中,D是边BC上的一点,已知∠ADC=∠DAC=2∠BAD,且BD=6,DC=5,那么△ABC的面积等于______.

∵∠ADC=∠DAC=2∠BAD
又∵∠ADC=∠ABD+∠DAB
∴∠ABD=∠DAB,
∴AD=BD=6
又∠ADC=∠DAC,得AC=CD=5.
△ADC的面积a=
×AD×
=
×6×4=12.
过A作AE⊥CD交CD于E,如右图,
则AE=
=
,
△ADB的面积b=
×AE×BD=
×
×6=14.4.
故△ABC的面积等于a+b=12+14.4=26.4.
又∵∠ADC=∠ABD+∠DAB
∴∠ABD=∠DAB,
∴AD=BD=6
又∠ADC=∠DAC,得AC=CD=5.
△ADC的面积a=
| 1 |
| 2 |
CD2-(
|
| 1 |
| 2 |
过A作AE⊥CD交CD于E,如右图,
则AE=
| 2a |
| CD |
| 24 |
| 5 |
△ADB的面积b=
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 5 |
故△ABC的面积等于a+b=12+14.4=26.4.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
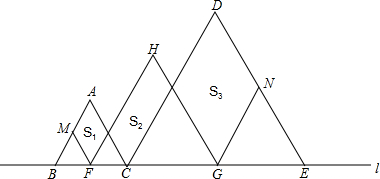 若S1+S3=10,则S2=______.
若S1+S3=10,则S2=______.