题目内容
（2013•东营）如图，已知直线l：y=
| ||
| 3 |
（0，42013）或（0，24026）
（0，42013）或（0，24026）
．分析：根据所给直线解析式可得l与x轴的夹角，进而根据所给条件依次得到点A1，A2的坐标，通过相应规律得到A2013坐标即可．
解答：解：∵直线l的解析式为：y=
x，
∴l与x轴的夹角为30°，
∵AB∥x轴，
∴∠ABO=30°，
∵OA=1，
∴AB=
，
∵A1B⊥l，
∴∠ABA1=60°，
∴AA1=3，
∴A1（0，4），
同理可得A2（0，16），
…，
∴A2013纵坐标为：42013，
∴A2013（0，42013）．
故答案为：（0，42013）或（0，24026）
| ||
| 3 |
∴l与x轴的夹角为30°，
∵AB∥x轴，
∴∠ABO=30°，
∵OA=1，
∴AB=
| 3 |
∵A1B⊥l，
∴∠ABA1=60°，
∴AA1=3，
∴A1（0，4），
同理可得A2（0，16），
…，
∴A2013纵坐标为：42013，
∴A2013（0，42013）．
故答案为：（0，42013）或（0，24026）
点评：本题考查的是一次函数综合题，先根据所给一次函数判断出一次函数与x轴夹角是解决本题的突破点；根据含30°的直角三角形的特点依次得到A、A1、A2、A3…的点的坐标是解决本题的关键．
练习册系列答案
相关题目
（2013•东营）如图，已知AB∥CD，AD和BC相交于点O，∠A=50°，∠AOB=105°，则∠C等于（ ）
（2013•东营）如图，正方形ABCD中，分别以B、D为圆心，以正方形的边长a为半径画弧，形成树叶形（阴影部分）图案，则树叶形图案的周长为（ ）
（2013•东营）如图，圆柱形容器中，高为1.2m，底面周长为1m，在容器内壁离容器底部0.3m的点B处有一蚊子，此时一只壁虎正好在容器外壁，离容器上沿0.3m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为
（2013•东营）如图，AB为⊙O的直径，点C为⊙O上一点，若∠BAC=∠CAM，过点C作直线l垂直于射线AM，垂足为点D．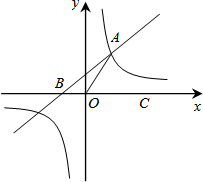
（2013•东营）如图，在平面直角坐标系中，一次函数y=nx+2（n≠0）的图象与反比例函数