Question

【题目】在边长为正方形中，点是上，且，点、是对角线上两点，且．当四边形周长最小时，则的值________．

Answer 1

【答案】

【解析】

根据题意得出作EF∥BD且EF=，连结AF交BD于N，在BD上截取MN=，此时四边形CEMN的周长最小，进而利用相似三角形的判定与性质得出答案．

作EF∥BD且EF=，连结AF交BD于N，在BD上截取MN=，延长AF交BC于P，作FQ⊥BC于Q，则四边形BMNE的周长最小，

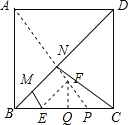
由∠FEQ=∠DBC=45°，可求得FQ=EQ=1，

∵∠APB=∠FPQ，∠ABP=∠FQP，

∴△PFQ∽△PAB，

∴，

∴，

解得：PQ=，

∴PB=3+=，

由对称性可求得tan∠BCN=tan∠PAB=．

∴cos∠BCN=.

故答案为．