题目内容
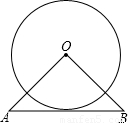
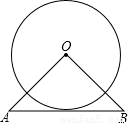
如图，△OAB是等腰直角三角形，∠AOB=90°，AB=8，且AB与⊙O相切，则⊙O的半径为 ．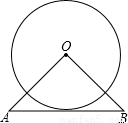
【答案】分析：连接OC，则OC是等腰直角△斜边上的高，因而OC=
AB，即可求解．
解答：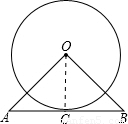
解：连接OC，
则OC⊥AB于点C．
∵△OAB是等腰直角三角形，
∴OC=
AB=4．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
AB，即可求解．解答：
解：连接OC，则OC⊥AB于点C．
∵△OAB是等腰直角三角形，
∴OC=
AB=4．点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
寒假学与练系列答案
相关题目
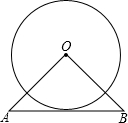如图，△OAB是等腰直角三角形，∠AOB=90°，AB=8，且AB与⊙O相切，则⊙O的半径为
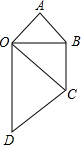如图，△OAB是等腰直角三角形，∠A=90°，AO=AB．以斜边OB为直角边，按顺时针方向画等腰直角三角形OBC，再以同样的方法画等腰直角三角形OCD．
