Question

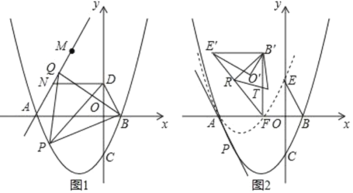
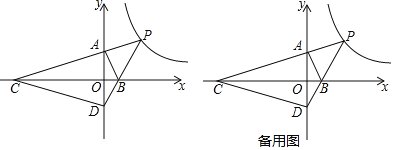
【题目】如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上．△AOB的两条外角平分线交于点P，P在反比例函数y的图象上．PA的延长线交x轴于点C，PB的延长线交y轴于点D，连接CD．

（1）求∠P的度数及点P的坐标；

（2）求△OCD的面积；

（3）△AOB的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．

Answer 1

【答案】（1）∠MPN＝90°，P（3，3）．（2）9；（3）27﹣18．

【解析】

（1）如图，作PM⊥OA于 M，PN⊥OB于N，PH⊥AB于H．利用全等三角形的性质解决问题即可．

（2）设OA=a，OB=b，则AM=AH=3-a，BN=BH=3-b，利用勾股定理求出a，b之间的关系，求出OC，OD即可解决问题．

（3）设OA=a，OB=b，则AM=AH=3-a，BN=BH=3-b，可得AB=6-a-b，推出OA+OB+AB=6，可得，利用基本不等式即可解决问题．

解：（1）如图，作PM⊥OA于M，PN⊥OB于N，PH⊥AB于H．

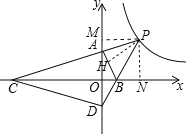
∴∠PMA＝∠PHA＝90°，

∵∠PAM＝∠PAH，PA＝PA，

∴△PAM≌△PAH（AAS），

∴PM＝PH，∠APM＝∠APH，

同理可证：△BPN≌△BPH，

∴PH＝PN，∠BPN＝∠BPH，

∴PM＝PN，

∵∠PMO＝∠MON＝∠PNO＝90°，

∴四边形PMON是矩形，

∴∠MPN＝90°，

∴∠APB＝∠APH+∠BPH（∠MPH+∠NPH）＝45°，

∵PM＝PN，

∴可以假设P（m，m），

∵P（m，m）在上，

∴m2＝9，

∵m＞0，

∴m＝3，

∴P（3，3）．

（2）设OA＝a，OB＝b，则AM＝AH＝3﹣a，BN＝BH＝3﹣b，

∴AB＝6﹣a﹣b，

∵AB2＝OA2+OB2，

∴a2+b2＝（6﹣a﹣b）2，

可得ab＝6a+6b﹣18，

∴3a+3b﹣9ab，

∵PM∥OC，

∴，

∴，

∴OC，同法可得OD，

∴.

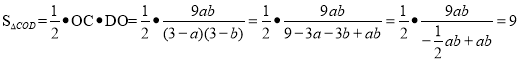（3）设OA＝a，OB＝b，则AM＝AH＝3﹣a，BN＝BH＝3﹣b，

∴AB＝6﹣a﹣b，

∴OA+OB+AB＝6，

∴，

∴，

∴，

∴，

∴，

∴，

∴△AOB的面积的最大值为：27﹣18．