题目内容
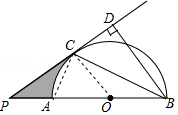
【题目】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC 
(1)求证:BC平分∠PBD;
(2)求证:PC2=PAPB;
(3)若PA=2,PC=2 ![]() ,求阴影部分的面积(结果保留π)
,求阴影部分的面积(结果保留π)
【答案】
(1)证明:连接OC,
∵PD切⊙O于点C,
∴OC⊥PD,
∵BD⊥PD,
∴BD∥OC,
∴∠DBC=∠BCO,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠CBD,
∴BC平分∠PBD
(2)证明:连接AC,
∵AB是半圆O的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=∠ACO+∠ABC=90°,
∵∠PCA+∠ACO=90°,
∴∠ACP=∠ABC,
∵∠P=∠P,
∴△ACP∽△CBP,
∴ ![]() ,
,
∴PC2=PAPB

(3)解:∵PC2=PAPB,PA=2,PC=2 ![]() ,
,
∴PB=6,
∴AB=4,
∴OC=2,PO=4,
∴∠POC=60°,
∴S阴影=S△POC﹣S扇形= ![]() 2
2 ![]() ×2﹣
×2﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)连接OC,由PD切⊙O于点C,得到OC⊥PD,根据平行线的性质得到∠DBC=∠BCO,根据的预计实现的性质得到∠OCB=∠OBC,等量代换得到∠OBC=∠CBD,于是得到即可;(2)连接AC,由AB是半圆O的直径,得到∠ACB=90°,推出∠ACP=∠ABC,根据相似三角形的性质即可得到结论;(3)根据图形的面积公式即可得到结果.
【考点精析】本题主要考查了角平分线的性质定理和切线的性质定理的相关知识点,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.