题目内容
如果方程(x-1)(x2-2x+m)=0的三根可以作为一个三角形的三边之长,那么实数m的取值范围是( )
| A.0≤m≤1 | B.m≥ | C. | D. ≤m≤1 ≤m≤1 |
C
∵方程(x-1)(x2-2x+m)=0的有三根,
∴x1=1,x2-2x+m=0有根,方程x2-2x+m=0的△=4-4m≥0,得m≤1.
又∵原方程有三根,且为三角形的三边和长.
∴有x2+x3>x1=1,|x2-x3|<x1=1,而x2+x3=2>1已成立;
当|x2-x3|<1时,两边平方得:(x2+x3)2-4x2x3<1.
即:4-4m<1.解得,m> .∴
.∴ <m≤1.故选C.
<m≤1.故选C.
∴x1=1,x2-2x+m=0有根,方程x2-2x+m=0的△=4-4m≥0,得m≤1.
又∵原方程有三根,且为三角形的三边和长.
∴有x2+x3>x1=1,|x2-x3|<x1=1,而x2+x3=2>1已成立;
当|x2-x3|<1时,两边平方得:(x2+x3)2-4x2x3<1.
即:4-4m<1.解得,m>
 .∴
.∴ <m≤1.故选C.
<m≤1.故选C.
练习册系列答案
相关题目


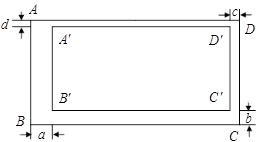
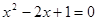 .
.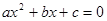 (a、b、c表示已知量,
(a、b、c表示已知量,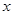 是未知数,a≠0),它的解的情况是:
是未知数,a≠0),它的解的情况是: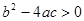 时,方程有两个不相等的解;
时,方程有两个不相等的解;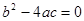 时,方程有两个相等的解(即一个解);
时,方程有两个相等的解(即一个解);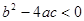 时,方程没有解;
时,方程没有解;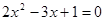 有几个解?为什么?
有几个解?为什么?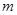 取何值时,关于
取何值时,关于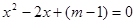 没有解?
没有解? 的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?
的无盖长方体箱子,且此长方体箱子的底面长比宽多2米,现已知购买这种铁皮每平方米需20元钱,问张大叔购回这张矩形铁皮共花了多少元钱?




 = __________
= __________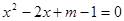 的一根是
的一根是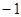 ,则
,则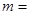 _______________ 。
_______________ 。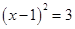 的解为 。
的解为 。