题目内容
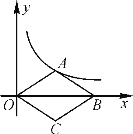
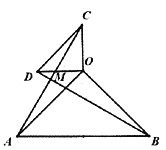
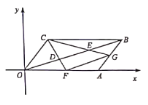
【题目】在平面直角坐标系中，平行四边形
的顶点
的坐标分别是
,
,点
把线段
三等分，延长
分别交
于点
,连接
, 则下列结论:
; 
③四边形
的面积为
;④
,其中正确的有（ ）.
A. 
B. 
C. 
D. 
【答案】C
【解析】
① 根据题意证明
，得出对应边成比例，再根据
把线段
三等分，证得
，即可证得结论；
② 延长BC交y轴于H，证明OA≠AB，则∠AOB≠∠EBG，所以△OFD∽△BEG不成立；
③ 利用面积差求得，根据相似三角形面积比等于相似比的平方进行计算并作出判断；
④ 根据勾股定理，计算出OB的长，根据三等分线段OB可得结论.
作AN⊥OB于点N，BM⊥x轴于点M，如图所示：
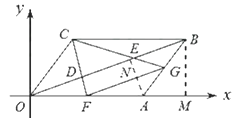
在平行四边形OABC中，点
的坐标分别是
,
,
∴
又∵把线段三等分，
∴
又∵
，
∴
∴
∴
即
，①结论正确；
∵
，
∴
∴平行四边形OABC不是菱形，
∴
∵
∴
∴
∴
故△OFD和△BEG不相似，故②错误；
由①得，点G是AB的中点，
∴FG是△span>OAB的中位线，
∴
，
又∵把线段三等分，
∴
∵
∴
∵
∴四边形DEGH是梯形
∴
，故③正确；
，故④错误；
综上：①③正确，
故答案为C.
练习册系列答案
相关题目
