题目内容
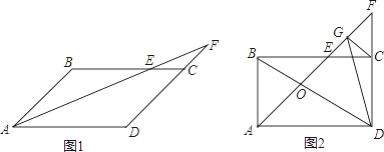
【题目】(1)问题发现:如图1,![]() 和
和![]() 均为等边三角形,点A,D,E在同一直线上,连接BE.
均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①![]() 的度数为 ;
的度数为 ;
②线段AD,BE之间的数量关系为 .
(2)拓展探究:如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点A,D,E在同一直线上,CM为
,点A,D,E在同一直线上,CM为![]() 中DE边上的高,连接BE,求
中DE边上的高,连接BE,求![]() 的度数,并说明理由.
的度数,并说明理由.

【答案】(1)①![]() ;②相等;(2)
;②相等;(2)![]() ,理由见解析
,理由见解析
【解析】
(1)①由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.②由△ACD≌△BCE,可得出答案.
(2)仿照(1)中的解法可求出∠AEB的度数.
解:(1)①∵∠ACB=∠DCE,∠DCB=∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
AC=BC,
∠ACD=∠BCE,,
∴△ACD≌△BCE,
∴AD=BE,![]() ,
,
∴![]() ;
;
②相等理由:
∵△ACD≌△BCE,
∴AD=BE.
故答案为:相等.
(2)![]() 理由:如图2,
理由:如图2,
∵![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
在在△ACD和△BCE中,
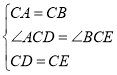 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°,
∵点A,D,E在同一直线上,
∴∠ADC=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=90°.

【题目】某校要从甲、乙两名同学中挑选一人参加创新能力大赛,在最近的五次选拔测试中, 他俩的成绩分别如下表,请根据表中数据解答下列问题:
第 1 次 | 第 2 次 | 第 3 次 | 第 4 次 | 第 5 次 | 平均分 | 众数 | 中位数 | 方差 | |
甲 | 60 分 | 75 分 | 100 分 | 90 分 | 75 分 | 80 分 | 75 分 | 75 分 | 190 |
乙 | 70 分 | 90 分 | 100 分 | 80 分 | 80 分 | 80 分 | 80 分 |
(1)把表格补充完整:
(2)在这五次测试中,成绩比较稳定的同学是多少;若将 80 分以上(含 80 分) 的成绩视为优秀,则甲、乙两名同学在这五次测试中的优秀率分别是多少;
(3)历届比赛表明,成绩达到80分以上(含 80分)就很可能获奖,成绩达到 90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.