题目内容
【题目】现场学习：在△ABC中，AB、BC、AC三边的长分别为
、
、
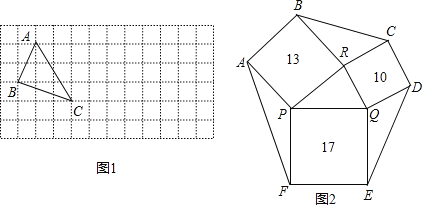
，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
（1）△ABC的面积为： _________ ；
（2）若△DEF三边的长分别为、
、
，请在图1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；
（3）如图2，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13，10，17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．
【答案】（1）
；（2）画图见解析，3；（3）62.
【解析】
试题（1）画出格子后可以根据格子的面积很容易的算出三角形的面积，大矩形的面积减去矩形内除去所求三角形的面积即可．
（2）构造时取（1，3）（2，2）（1，4）即可．
（3）根据PRQ的长度取（1，3）（1，4）（2，3）在网格中画图，求出其面积．
试题解析：（1）根据格子的数可以知道面积为S=3×3-
(1×2+1×3+2×3)=；
（2）画图为
计算出正确结果S△DEF=2×4-（1×2+1×4+2×2）=3；
（3）利用构图法计算出S△PQR=
，
△PQR、△BCR、△DEQ、△AFP的面积相等，
计算出六边形花坛ABCDEF的面积为S正方形PRBA+S正方形RQDC+S正方形QPFE+4S△PQR=13+10+17+4×=62．
【题目】某商场销售一种商品，进价为每个20元，规定每个商品售价不低于进价，且不高于60元，经调查发现，每天的销售量y（个）与每个商品的售价x（元）满足一次函数关系，其部分数据如下所示：
每个商品的售价x（元） | … | 30 | 40 | 50 | … |
每天的销售量y（个） | 100 | 80 | 60 | … |
（1）求y与x之间的函数表达式；
（2）设商场每天获得的总利润为w（元），求w与x之间的函数表达式；
（3）不考虑其他因素，当商品的售价为多少元时，商场每天获得的总利润最大，最大利润是多少？
