Question

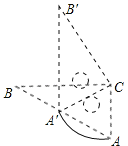
【题目】如图，已知AB，CD为⊙O的直径，过点A作弦AE垂直于直径CD于F，点B恰好为弧DE的中点，连接BC，BE.

(1)求证：AE=BC；

(2)若AE=，求⊙O的半径；

(3)在(2)的条件下，求阴影部分的面积.

Answer 1

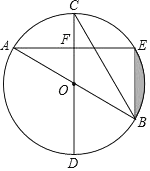
【答案】（1）证明见解析;（2）半径为2;（3）

【解析】

（1）连接BD，证明△ABE≌△CDB即可；

（2）根据垂径定理和圆周角定理易求得∠A=∠ABE，得出∠A=30°，解直角三角形求得AB，即可求得⊙O的半径；

（3）根据S阴影=S扇形BOE-S△BOE求得即可．

（1）连接BD，如图，

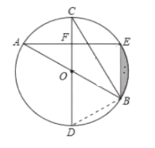
∵AB，CD为的直径，

∴∠CBD=∠AEB=90°，

∵点B恰好为的中点，

∴，

∴∠A=∠C，

∵AB，CD为⊙O的直径，

∴AB=CD，

∴在△ABE和△CDB中，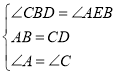

∴△ABE≌△CDB，

∴AE=BC；

（2）∵过点A作弦AE垂直于直径CD于F，

∴，

由（1）可得∠ABE=∠CDB，

∴，

∴，

∴∠A=∠ABE，

又∵∠AEB=90°，

∴∠A=30°，∠ABE=60°，

在Rt△ABE中，cos∠BAE=，

∴AB=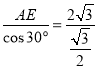=4，

∴⊙O的半径是：×4=2；

（3）连接OE，过点O作OM⊥BE于点M，如图，

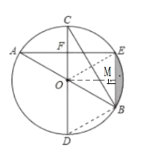
∵∠A=30°，

∴∠EOB=2∠A=2×30°=60°，

又∵OB=OE=2，

∴△BOE是等边三角形，

∴OB=BE=OE=2，∠BOE=60°，

又∵OM⊥BE，

∴BM=BE=1，

∴OM==，

∴S△EOB=×2×=，

∴S阴影=S扇形BOE-S△BOE=-=．