Question

24、如图所示，已知△ACM和△CBN都是等边三角形，点A、C、B在同一直线上，连接AN、MB．
（1）求证：AN=BM；
（2）若等边三角形CBN绕顶点C顺时针旋转后（旋转角α＜180°），此时AN与BM是否还相等？若相等，给出证明；若不相等，说明理由．

Answer 1

分析：（1）由△ACM和△CBN是等边三角形，所以，AC=MC，CB=CN；∠ACM=∠NCB=60°，∠MCN=60°，∠ACN=∠MCB=120°，求△ACN≌△MCB，得出结论；
（2）结合图形做题．根据等边三角形的性质求三角形全等再结合图形做题．

解答：解：（1）证明：在三角形ACM和NCB中，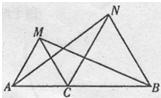
因为，△ACM和△CBN是等边三角形，
所以AC=MC，CB=CN，∠ACM=∠BCN=60°，
所以∠ACM+∠MCN=∠BCN+∠MCN，即∠ACN=∠MCB，
所以△ACN≌△MCB（SAS）
所以，AN=BM．
（2）解：AN与BM相等．
旋转角为α，
当0°≤α＜60°时，如下图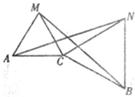

因为，△ACM和△CBN是等边三角形，
所以，AC=MC，CB=CN．
∠ACN=60°+∠MCN
∠MCB=60°+∠MCN
∠ACN=∠MCB．
所以，△ACN≌△MCB．
所以，AN=BM．
当α=60°时，A、C、N三点共线，M、C、B三点共线，
AN=AC+CN，BM=MC+CB=AC+CN
所以，AN=BM．
当60°＜α＜180°时，如下图，
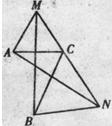因为，△ACM和△CBN是等边三角形，
所以，AC=MC，CB=CN．
∠ACN=60°+∠ACB
∠MCB=60°+∠ACB
∠ACN=∠MCB
∴△ACN≌△MCB
∴AN=BM．

点评：本题考查了全等三角形的判定与性质及等边三角形的性质；可围绕结论寻找全等三角形，运用全等三角形的性质判定线段相等，进行分情况讨论是正确解答本题的关键．