题目内容
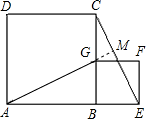
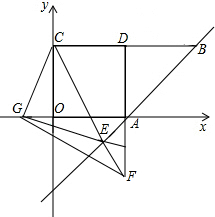
 已知:如图,正方形BEFG的边BG在正方形ABCD的边BC上,连接AG、EC.
已知:如图,正方形BEFG的边BG在正方形ABCD的边BC上,连接AG、EC.
(1)观察猜想图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程;若不存在,请说明理由.
(2)观察猜想AG与CE之间的大小关系,并说明你的理由;
(3)请你延长AG交CE于点M,AM与CE是什么样的位置关系?请说明理由.
 解:(1)存在,△BCE绕B逆时针旋转90°得到△BAG;
解:(1)存在,△BCE绕B逆时针旋转90°得到△BAG;(2)AG=CE.
理由是:∵四边形ABCD和四边形BGFE都是正方形,
∴AB=BC,∠GBA=∠EBC=90°,BG=BE.
在△ABG与△CBE中,
 ,
,∴△ABG≌△CBE,
∴AG=CE;
(3)AM⊥CE.
理由是:∵△ABG≌△CBE,
∴∠GAB=∠BCE,
∵∠CGM=∠AGB,
∵∠ABG=90°,
∴∠GAB+∠AGB=90°,
∴∠GCM+∠CGM=90°,
∴∠CMG=90°,
∴AM⊥CE.
分析:(1)根据旋转性质求出即可;
(2)根据正方形的性质求出AB=BC,∠GBA=∠CBE=90°,BG=BE,根据SAS求出即可;
(3)根据全等推出∠GAB=∠BCE,求出∠GCM+∠CGM=90°即可.
点评:本题主要考查对正方形的性质,旋转的性质,全等三角形的性质和判定等知识点的理解和掌握,能求出△ABG≌△CBE是解此题的关键.

练习册系列答案
相关题目
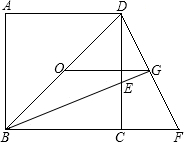 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.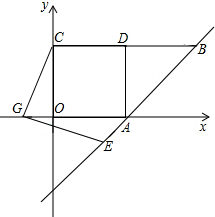
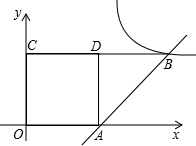



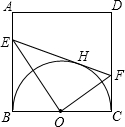 于E,交CD于F.
于E,交CD于F.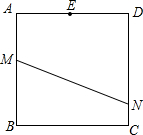 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.