题目内容
【题目】如图，抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．
（1）求A、B、C的坐标；
（2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N．若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ．过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG=2 
DQ，求点F的坐标．
【答案】
（1）
解：由抛物线y=﹣x2﹣2x+3可知，C（0，3），
令y=0，则0=﹣x2﹣2x+3，解得x=﹣3或x=1，
∴A（﹣3，0），B（1，0）
（2）
解：方法一：由抛物线y=﹣x2﹣2x+3可知，对称轴为x=﹣1，
设M点的横坐标为m，则PM=﹣m2﹣2m+3，MN=（﹣m﹣1）×2=﹣2m﹣2，
∴矩形PMNQ的周长=2（PM+MN）=（﹣m2﹣2m+3﹣2m﹣2）×2=﹣2m2﹣8m+2=﹣2（m+2）2+10，
∴当m=﹣2时矩形的周长最大．
∵A（﹣3，0），C（0，3），设直线AC解析式为y=kx+b，
解得k=1，b=3，
∴解析式y=x+3，当x=﹣2时，则E（﹣2，1），
∴EM=1，AM=1，
∴S= 
AMEM=
方法二：
设P（t，﹣t2﹣2t+3），Q（﹣2﹣t，﹣t2﹣2t+3），
∴矩形PQMN周长为：2PQ+2PM，
∴2PQ+2PM=2（﹣2﹣t﹣t）+2（﹣t2﹣2t+3），
∴2PQ+2PM=﹣2t2﹣8t+2，
∴当t=﹣2时，周长最大，
∴P（﹣2，3），
∵A（﹣3，0），C（0，3），
∴lAC：y=x+3，
∵点E在直线AC上，且EX=PX，
把x=﹣2代入，
∴E（﹣2，1），
∴S△AEM= AM×EM= ×1×1=
（3）
解：方法一：∵M点的横坐标为﹣2，抛物线的对称轴为x=﹣1，
∴N应与原点重合，Q点与C点重合，
∴DQ=DC，
把x=﹣1代入y=﹣x2﹣2x+3，解得y=4，
∴D（﹣1，4）
∴DQ=DC= 
，
∵FG=2 DQ，
∴FG=4，
设F（n，﹣n2﹣2n+3），
则G（n，n+3），
∵点G在点F的上方，
∴（n+3）﹣（﹣n2﹣2n+3）=4，
解得：n=﹣4或n=1．
∴F（﹣4，﹣5）或（1，0）
方法二：
∵D为抛物线顶点，∴D（﹣1，4），Q（0，3），
∴DQ= 
，
∵FG=2 DQ=2 × =4，
∴t2+3t﹣4=0，
∴t1=﹣4，t2=1，
∴F1（﹣4，﹣5），F2（1，0）
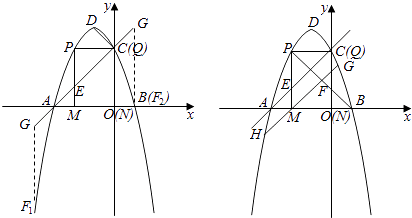
【解析】方法一：（1）通过解析式即可得出C点坐标，令y=0，解方程得出方程的解，即可求得A、B的坐标．（2）设M点横坐标为m，则PM=﹣m2﹣2m+3，MN=（﹣m﹣1）×2=﹣2m﹣2，矩形PMNQ的周长d=﹣2m2﹣8m+2，将﹣2m2﹣8m+2配方，根据二次函数的性质，即可得出m的值，然后求得直线AC的解析式，把x=m代入可以求得三角形的边长，从而求得三角形的面积．（3）设F（n，﹣n2﹣2n+3），根据已知若FG=2 DQ，即可求得．
方法二：（1）略．（2）求出P，Q的参数坐标，并得出周长的函数表达式，求出P点，进而求出E点坐标，并求出△AEM的面积．（3）求出D点坐标，并求出DQ长度；再求出F，G的参数坐标，并得到FG的函数表达式，利用FG=DQ，求点F的坐标．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
