题目内容
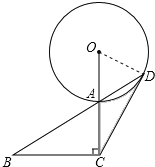
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.

【答案】(1)见解析;(2)S阴影=2![]() ﹣
﹣![]() π.
π.
【解析】
(1)连接OD,求出∠OAD=60°,得出等边三角形OAD,求出AD=OA=AC,∠ODA=∠O=60°,求出∠ADC=∠ACD=![]() ∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
∠OAD=30°,求出∠ODC=90°,根据切线的判定得出即可;
(2)求出OD,根据勾股定理求出CD长,分别求出三角形ODC和扇形AOD的面积,相减即可.
(1)证明:连接OD,
∵∠BCA=90°,∠B=30°,
∴∠OAD=∠BAC=60°,
∵OD=OA,
∴△OAD是等边三角形,
∴AD=OA=AC,∠ODA=∠O=60°,
∴∠ADC=∠ACD=![]() ∠OAD=30°,
∠OAD=30°,
∴∠ODC=60°+30°=90°,
即OD⊥DC,
∵OD为半径,
∴CD是⊙O的切线;
(2)解:∵AB=4,∠ACB=90°,∠B=30°,
∴OD=OA=AC=![]() AB=2,
AB=2,
由勾股定理得:CD=![]()
∴S阴影=S△ODC﹣S扇形AOD=![]() .
.

 期末冲刺100分创新金卷完全试卷系列答案
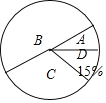
期末冲刺100分创新金卷完全试卷系列答案【题目】某市将开展演讲比赛活动,某校对参加选拔的学生的成绩按A、B、C、D四个等级进行统计,绘制了如下不完整的统计表和扇形统计图,
成绩等级 | 频数 | 频率 |
A | 4 | n |
B | m | 0.51 |
C | ||
D | 15 |
(1)求m、n的值;
(2)求“C等级”所对应的扇形圆心角的度数;
(3)已知成绩等级为A的4名学生中有1名男生和3名女生,现从中随机挑选2名学生代表学校参加全市比赛,求出恰好选中一男生和一女生的概率
【题目】某校举行了创建全国文明城市知识竞赛活动,初一年级全体同学参加了竞赛.收集数据:现随机抽取初一年级30名同学“创文知识竞赛”成绩,分数如下(单位:分):
90 | 85 | 68 | 92 | 81 | 84 | 95 | 93 | 87 | 89 | 78 | 99 | 89 | 85 | 97 |
88 | 81 | 95 | 86 | 98 | 95 | 93 | 89 | 86 | 84 | 87 | 79 | 85 | 89 | 82 |
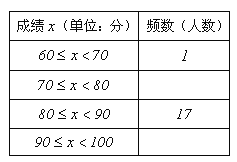

⑴请将图表中空缺的部分补充完整;
⑵学校决定表彰“创文知识竞赛”成绩在90分以上的同学,根据上表统计结果估计该校初一年级360人中,约有多少人将获得表彰;
⑶“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .