题目内容
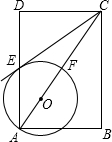
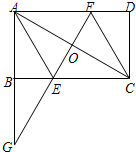 如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB到点G,使BG=AB,连结GO交BC于点E,延长GO交AD于点F.
如图,在矩形ABCD中,点O是AC的中点,AC=2AB,延长AB到点G,使BG=AB,连结GO交BC于点E,延长GO交AD于点F.(1)求证:四边形AECF是菱形;
(2)连结CG,若AE=3cm,延长AE交线段CG于点M,求AM的长.
分析:(1)根据中点定义可得AC=2AO,然后求出AO=AB,AC=AG,再利用“边角边”证明△AOG和△ABC全等,根据全等三角形对应角相等可得∠ABC=∠AOG=90°,再利用“角边角”证明△AOF和△COE全等,根据全等三角形对应边相等可得AF=CE,然后求出四边形AECF为平行四边形,最后根据对角线互相垂直的平行四边形是菱形证明;
(2)先求出∠ACB=30°,再根据菱形的性质EA=EC,然后根据等边对等角求出∠EAO=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出OE,再利用勾股定理列式计算求出AO,从而得到AC的长度,然后求出∠CAE=∠GAE=30°,根据等腰三角形三线合一的性质以及直角三角形30°角所对的直角边等于斜边的一半求出CM,再利用勾股定理列式计算即可求出AM.
(2)先求出∠ACB=30°,再根据菱形的性质EA=EC,然后根据等边对等角求出∠EAO=30°,根据直角三角形30°角所对的直角边等于斜边的一半求出OE,再利用勾股定理列式计算求出AO,从而得到AC的长度,然后求出∠CAE=∠GAE=30°,根据等腰三角形三线合一的性质以及直角三角形30°角所对的直角边等于斜边的一半求出CM,再利用勾股定理列式计算即可求出AM.
解答:(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,
∴∠FAO=∠ECO,
又∵BG=AB,AC=2AB,O为AC中点,
∴AO=CO=AB,AC=AG,
在△AOG和△ABC中,
,
∴△AOG≌△ABC(SAS),
∴∠ABC=∠AOG=90°,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF为平行四边形,
又∵AC⊥EF,
∴四边形AECF为菱形;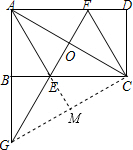
(2)在Rt△ABC中,由AB=
AC可推出∠ACB=30°,
由菱形可得EA=EC,
∴∠EAO=30°,
∵AE=3cm,
∴OE=
AE=
cm,AO=
=
=
cm,
AC=2AO=3
cm,
延长AE交CG于点M,∵AC=AG且∠CAE=∠GAE=30°,
∴AM⊥CG,
∴CM=
AC=
cm,
∴AM=
=
=
cm.
∴AD∥BC,
∴∠FAO=∠ECO,
又∵BG=AB,AC=2AB,O为AC中点,
∴AO=CO=AB,AC=AG,
在△AOG和△ABC中,
|
∴△AOG≌△ABC(SAS),
∴∠ABC=∠AOG=90°,
在△AOF和△COE中,
|
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF为平行四边形,
又∵AC⊥EF,
∴四边形AECF为菱形;

(2)在Rt△ABC中,由AB=
| 1 |
| 2 |
由菱形可得EA=EC,
∴∠EAO=30°,
∵AE=3cm,
∴OE=
| 1 |
| 2 |
| 3 |
| 2 |
| AE2-OE2 |
32-(
|
3
| ||
| 2 |
AC=2AO=3
| 3 |
延长AE交CG于点M,∵AC=AG且∠CAE=∠GAE=30°,
∴AM⊥CG,
∴CM=
| 1 |
| 2 |
3
| ||
| 2 |
∴AM=
| AC2-CM2 |
(3
|
| 9 |
| 2 |
点评:本题考查了矩形的性质,全等三角形的判定与性质,菱形的判定与性质,熟记各图形的性质与判定方法找出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
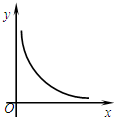
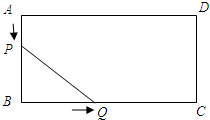 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )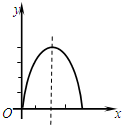
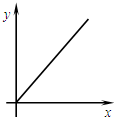
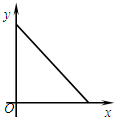
 .
.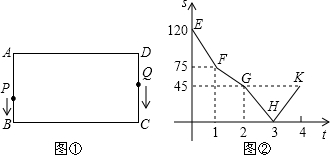 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.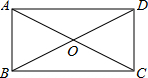 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )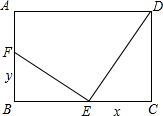 DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.