Question

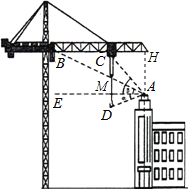
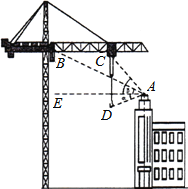
【题目】为了给学生提供更好的学习生活环境，重庆一中寄宿学校2015年对校园进行扩建．某天一台塔吊正对新建教学楼进行封顶施工，工人在楼顶A处测得吊钩D处的俯角α=22°，测得塔吊B，C两点的仰角分别为β=27°，γ=50°，此时B与C距3米，塔吊需向A处吊运材料．（tan27°≈0.5，tan50°≈1.2，tan22°≈0.4）

（1）吊钩需向右、向上分别移动多少米才能将材料送达A处？

（2）封顶工程完毕后需尽快完成新建教学楼的装修工程．如果由甲、乙两个工程队合做，12天可完成；如果由甲、乙两队单独做，甲队比乙队少用10天完成．求甲、乙两工程队单独完成此项工程所需的天数．

Answer 1

【答案】（1）吊钩需向右、向上分别移动米、米才能将材料送达A处；（2）甲单独做20天完成此工程，则乙单独做3．天完成此工程．

【解析】

试题分析：（1）过点A作AH⊥BC于点H，则△AHC，△AHB均为Rt△，设CH=x，在△ACH与△ABH中分别用x表示出AH的长，故可得出x的值，进而可得出AM与DM的长，由此得出结论；

（2）设甲单独做y天完成此工程，则乙单独做（y+10）天完成此工程，由甲、乙两个工程队合做，12天可完成求出y的值，进而可得出结论．

解：（1）过点A作AH⊥BC于点H，则△AHC，△AHB均为Rt△，设CH=x，

∵HC∥AE，

∴∠HCA=γ=50°，

∴AH=xtan50°=1.2x．

∵HB∥AE，

∴∠HBA=β=27°，

∴在Rt△ABH中，AH=BHtan27°，即1.2x=（x+3）tan27°，即1.2x=（x+3），解得x=．

∵四边形AHCM是矩形，

∴AM=．

在Rt△AMD中，DM=AMtan22°=×0.4=．

答：吊钩需向右、向上分别移动米、米才能将材料送达A处；

（2）设甲单独做y天完成此工程，则乙单独做（y+10）天完成此工程，

由题意得，+=，解得y1=20，y2=﹣6（舍去）．

经检验，y=20是原分式方程的解且符合题意，

故乙单独完成此项工程的天数为10+20=30（天）．

答：甲单独做20天完成此工程，则乙单独做3．天完成此工程．