题目内容
 如图,D是△ABC中BC边上一点,AB=AC=BD,则∠1和∠2的关系是
如图,D是△ABC中BC边上一点,AB=AC=BD,则∠1和∠2的关系是
- A.∠1=2∠2
- B.∠1+∠2=90°
- C.180°-∠1=3∠2
- D.180°+∠2=3∠1
D
分析:先根据AB=AC=BD可求出∠B=∠C,∠1=∠BAD,再根据三角形内角和定理可得∠B+2∠1=180°,由三角形内角与外角的性质可得∠1=∠2+∠C,再把①代入②即可.
解答:∵AB=AC=BD,
∴∠B=∠C,∠1=∠BAD,
又∵∠B+2∠1=180°,∠1=∠2+∠C,∠B=∠C,
∴∠B=180°-2∠1,
∴∠1=∠2+180°-2∠1,
即180°+∠2=3∠1.
故选D.
点评:本题涉及到三角形内角与外角的关系、三角形内角和定理及等腰三角形的性质,涉及面较广,但难度适中.
分析:先根据AB=AC=BD可求出∠B=∠C,∠1=∠BAD,再根据三角形内角和定理可得∠B+2∠1=180°,由三角形内角与外角的性质可得∠1=∠2+∠C,再把①代入②即可.
解答:∵AB=AC=BD,
∴∠B=∠C,∠1=∠BAD,
又∵∠B+2∠1=180°,∠1=∠2+∠C,∠B=∠C,
∴∠B=180°-2∠1,
∴∠1=∠2+180°-2∠1,
即180°+∠2=3∠1.
故选D.
点评:本题涉及到三角形内角与外角的关系、三角形内角和定理及等腰三角形的性质,涉及面较广,但难度适中.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( )
8、如图,DE是△ABC中边AC的垂直平分线,若BC=18cm,AB=10cm,则△ABD的周长为( )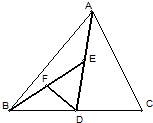 13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于
13、如图,AD是△ABC中BC边上的中线,E,F分别是AD、BE的中点,若△BFD的面积为6,则△ABC的面积等于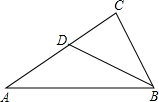 如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( )
如图,D是△ABC中AC边上的一点,根据下列条件不可推出△BDC∽△ABC的是( )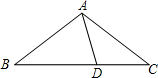 如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( )
如图,D是△ABC中BC边上一点,AB=AC=BD,AD=DC,则∠B的度数是( )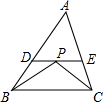 如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=
如图,P是△ABC中∠B,∠C两角平分线的交点,过点P作DE∥BC,分别与AB、AC交于点D、E,DE=10,则DB+EC=