题目内容
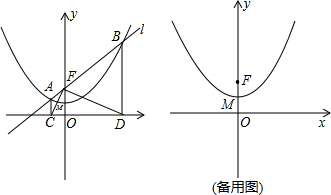
(2013•莆田质检)已知:抛物线y=
x2+1的顶点为M,直线l过点F(0,2)且与抛物线分别相交于A、B两点.过点A、B分别作x轴的垂线,垂足分别为点C、D,连接CF、DF.
(1)如图:
①若A(-1,
),求证:AC=AF;
②若A(m,n),判断以CD为直径的圆与直线l的位置关系.并加以证明.
(2)若直线l绕点F旋转,且与x轴交于点P,PC×PD=8.求直线l的解析式.
| 1 |
| 4 |
(1)如图:
①若A(-1,
| 5 |
| 4 |
②若A(m,n),判断以CD为直径的圆与直线l的位置关系.并加以证明.
(2)若直线l绕点F旋转,且与x轴交于点P,PC×PD=8.求直线l的解析式.

分析:(1)①利用勾股定理列式求出AF,即可得证;
②把A点坐标代入抛物线用m表示出n,然后利用待定系数法求一次函数解析式求出直线AB的解析式,与抛物线联立求解得到点B的坐标,再利用勾股定理列式求出BF,得到BF=BD,过点B作BE⊥DF交x轴于E,根据等腰三角形三线合一的性质可得∠EBF=∠EBD,再利用“边角边”证明△BEF和△BED全等,根据全等三角形对应角相等可得∠BFE=∠BDE=90°,全等三角形对应边相等可得EF=ED,连接AE,利用“HL”证明△ACE和△AFE全等,根据全等三角形对应边相等可得EF=CE,从而得到EF=
CD,然后根据直线与圆相切的定义解答;
(2)根据切割线定理可得PF2=PC•PD,再利用勾股定理列式求出OP的长,写出点P的坐标,再利用待定系数法求一次函数解析式分两种情况解答.
②把A点坐标代入抛物线用m表示出n,然后利用待定系数法求一次函数解析式求出直线AB的解析式,与抛物线联立求解得到点B的坐标,再利用勾股定理列式求出BF,得到BF=BD,过点B作BE⊥DF交x轴于E,根据等腰三角形三线合一的性质可得∠EBF=∠EBD,再利用“边角边”证明△BEF和△BED全等,根据全等三角形对应角相等可得∠BFE=∠BDE=90°,全等三角形对应边相等可得EF=ED,连接AE,利用“HL”证明△ACE和△AFE全等,根据全等三角形对应边相等可得EF=CE,从而得到EF=
| 1 |
| 2 |
(2)根据切割线定理可得PF2=PC•PD,再利用勾股定理列式求出OP的长,写出点P的坐标,再利用待定系数法求一次函数解析式分两种情况解答.
解答:(1)证明:①∵F(0,2),A(-1,
),
∴AF=
=
,
又∵AC=
,
∴AC=AF;
②∵点A(m,n)在抛物线y=
x2+1,
∴n=
m2+1,
设直线AB得到解析式为y=kx+b(k≠0),
则
,
解得
,
∴直线AB的解析式为y=(
-
)x+2,
联立
,
解得
(为点A坐标),
,
∴点B坐标为(-
,
+1),
由勾股定理得,BF=
=
=
+1,
∴BF=BD,
过点B作BE⊥DF交x轴于E,
则∠EBF=∠EBD,
在△BEF和△BED中,
,
∴△BEF≌△BED(SAS),
∴∠BFE=∠BDE=90°,EF=ED,
∴EF⊥直线l,
连接AE,
在△ACE和△AFE中,
,
∴△ACE≌△AFE(HL),
∴EF=CE,
∴EF=
CD,
∴点E为以CD为直径的圆的圆心,以CD为直径的圆与直线l相切;
(2)解:由切割线定理,PF2=PC•PD,
∵PC•PD=8,
∴PF2=8,
∴PO=
=
=2,
∴点P的坐标为(2,0)或(-2,0),
设直线l的解析式为y=kx+b(k≠0),
当P(2,0)时,
,
解得
,
所以,直线l的解析式为y=-x+2,
当P(-2,0)时,
,
解得
,
所以,直线l的解析式为y=x+2,
综上所述,直线l的解析式为y=-x+2或y=x+2.
| 5 |
| 4 |
∴AF=
(-1-0)2+(
|
| 5 |
| 4 |
又∵AC=
| 5 |
| 4 |
∴AC=AF;
②∵点A(m,n)在抛物线y=
| 1 |
| 4 |
∴n=
| 1 |
| 4 |
设直线AB得到解析式为y=kx+b(k≠0),
则
|
解得
|
∴直线AB的解析式为y=(
| m |
| 4 |
| 1 |
| m |
联立
|
解得
|
|
∴点B坐标为(-
| 4 |
| m |
| 4 |
| m2 |

由勾股定理得,BF=
(-
|
(
|
| 4 |
| m2 |
∴BF=BD,
过点B作BE⊥DF交x轴于E,
则∠EBF=∠EBD,
在△BEF和△BED中,
|
∴△BEF≌△BED(SAS),
∴∠BFE=∠BDE=90°,EF=ED,
∴EF⊥直线l,
连接AE,
在△ACE和△AFE中,
|
∴△ACE≌△AFE(HL),
∴EF=CE,
∴EF=
| 1 |
| 2 |
∴点E为以CD为直径的圆的圆心,以CD为直径的圆与直线l相切;
(2)解:由切割线定理,PF2=PC•PD,
∵PC•PD=8,
∴PF2=8,
∴PO=
| PF2-OF2 |
| 8-22 |
∴点P的坐标为(2,0)或(-2,0),
设直线l的解析式为y=kx+b(k≠0),
当P(2,0)时,
|
解得
|
所以,直线l的解析式为y=-x+2,
当P(-2,0)时,
|
解得
|
所以,直线l的解析式为y=x+2,
综上所述,直线l的解析式为y=-x+2或y=x+2.
点评:本题是二次函数综合题型,主要利用了勾股定理,待定系数法求一次函数解析式,直线与圆的位置,切割线定理,本题难点在于(1)②作出EF并求出EF⊥直线l并且EF=
CD,(2)要注意分情况讨论.
| 1 |
| 2 |

练习册系列答案
相关题目
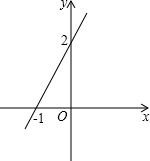 (2013•莆田质检)如图是一次函数y=kx+b的图象,则方程kx+b=0的解为
(2013•莆田质检)如图是一次函数y=kx+b的图象,则方程kx+b=0的解为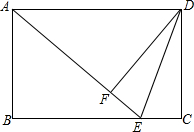 (2013•莆田质检)如图,在矩形ABCD中,E是BC边上的点,将△DCE沿DE折叠,使点C落在AE边上的点F处.
(2013•莆田质检)如图,在矩形ABCD中,E是BC边上的点,将△DCE沿DE折叠,使点C落在AE边上的点F处. (2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F.
(2013•莆田质检)如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,点E是AB上一点,以AE为直径的⊙O过点D,且交AC于点F. (2013•莆田质检)如图,一次函数
(2013•莆田质检)如图,一次函数