题目内容

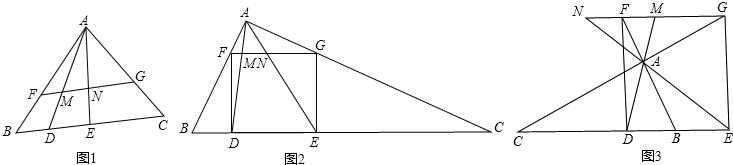
（1）如图1，在△ABC中，点D，E在边BC上，BD：DE：CE=1：2：3，线段FG∥BC，分别交线段AD，AE于M、N两点，则有FM：MN：NG=
1：2：3
1：2：3

（2）如图2，在△ABC中，∠BAC=90°，正方形DEGF的四个顶点有△ABC的三边上，线段FG分别交线段AD，AE于M、N两点，若BD=4，EC=9，求MN的长？
（3）如图3，在△ABC中，∠BAC=90°，正方形DEGF的四个顶点在△ABC的三边所在的直线上，DA与EN的延长线分别交直线FG于M、N两点，求证：MN2=MF•NG．
分析：（1）根据平行线分线段成比例定理列式求出
FM
BD
=
AM
AD
，
MN
DE
=
AM
AD
=
AN
AE
，
NG
CE
=
AN
AE
，然后表示出FM、MN、NG，再求出比值即可；
（2）根据同角的余角相等求出∠B=∠CGE，然后求出△BDF和△GEC相似，再根据相似三角形对应边成比例列式求正方形DEGF的边长，然后求出
GF
BC
，再根据相似三角形对应边成比例列式求出MF、NG，然后根据MN=FG-MF-NG代入数据计算即可得解；
（3）根据平行线分线段成比例定理列式表示出MF、NG，然后求出MF•NG，再求出△BDF和△GEC相似，利用相似三角形对应边成比例列式求出BD•CE=DE2，整理即可得证．
解答：（1）解：∵FG∥BC，
∴
FM
BD
=
AM
AD
，
MN
DE
=
AM
AD
=
AN
AE
，
NG
CE
=
AN
AE
，
∴
FM
BD
=
MN
DE
=
NG
CE
，
设
FM
BD
=
MN
DE
=
NG
CE
=k，
则FM=kBD，MN=kDE，NG=kCE，
∵BD：DE：CE=1：2：3，
∴FM：MN：NG=kBD：kDE：kCE=1：2：3，
 
（2）解：∵∠BAC=90°，
∴∠B+∠C=90°，
∵四边形DEGF是正方形，
∴∠C+∠CGE=90°，DF=EG，
∴∠B=∠CGE，
又∵∠BDF=∠GEC=90°，
∴△BDF∽△GEC，
∴
BD
EG
=
DF
EC
，
∵BD=4，EC=9，
∴EG•DF=EG2=BD•EC=4×9=36，
∴EG=6，
即正方形DEGF的边长为6，
∵正方形DEGF的边FG∥DE，
∴
AF
AB
=
AG
AC
=
FG
BC
=
6
4+6+9
=
6
19
，
MF
BD
=
AF
AB
，
NG
EC
=
AG
AC
，
即
MF
4
=
6
19
，
NG
9
=
6
19
，
解得MF=
24
19
，NG=
54
19
，
∴MN=FG-MF-NG=6-
24
19
-
54
19
=
36
19
；

（3）证明：在正方形DEGF中，DE∥FG，
∴CE∥NG，
∴
MF
BD
=
AM
AD
，
MN
DE
=
AM
AD
=
AN
AE
，
NG
CE
=
AN
AE
，
∴
MF
BD
=
MN
DE
=
NG
CE
，
∴MF=
BD
DE
•MN，NG=
CE
DE
•MN，
∴MF•NG=
BD
DE
•MN•
CE
DE
•MN=MN2•
BD•CE
DE2
，
∵∠BAC=90°，四边形DEFG是正方形，
∴∠C+∠ABC=90°，∠BFD+∠ABC=90°，GE=DF=DE，
∴∠C=∠BFD，
又∵∠BAC=∠GEC=90°，
∴△BDF∽△GEC，
∴
BD
GE
=
DF
CE
，
∴BD•CE=GE•DF=DE2，
∴
BD•CE
DE2
=1，
∴MN2=MF•NG．
故答案为：1：2：3．
点评：本题考查了相似形综合题，主要利用了平行线分线段成比例定理，相似三角形的判定与性质，综合题，但难度不大，要注意比例相等的联系．
练习册系列答案
相关题目
如图，要在一个圆形工件通过画直径来确定圆心，下列四种工具和确定方法不能找到圆心的是（　　）
如图1，在Rt△ABC中，∠C=90°，BC=8厘米，点D在AC上，CD=3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒k厘米，行完AC全程用时8秒；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒（0＜x＜8）DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．
（1）求y1与x的函数关系，并在图2中画出y1的图象；
（2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求AC的长；
（3）在图2中，点G是x轴正半轴上一点，且0＜OG＜4，过G作EF垂直于x轴，分别交y1、y2的图象于点E、F．
①说出线段EF的长在图1中所表示的实际意义；
②线段EF长有可能等于3吗？若能，请求出相应的x的值，若不能请说明理由．
如图1，在一条笔直地公路上有A、B、C三地，B、C两地相距150km，甲、乙两辆汽车分别从B、C两地同时出发，沿公路匀速相向而行，分别驶往C、B两地．甲、乙两车到A地的距离y1、y2与行驶时间x（h）的函数图象如图2所示．（乙：折线E-M-P）

（1）请在图1中标出A地的大致位置；
（2）图2中，点M的坐标是
（1.2，0）
（1.2，0）
，该点的实际意义是
点M表示乙车1.2小时到达A地
点M表示乙车1.2小时到达A地
；
（3）求甲车到A地的距离y1与行驶时间x（h）的函数关系式，直接写出乙车到A地的距离y2与行驶时间x（h）的函数关系式，并在图2中补全甲车的函数图象；
（4）A地设有指挥中心，指挥中心与两车配有对讲机，两部对讲机在15km之内（含15km）时能够互相通话，直接写出两车可以同时与指挥中心用对讲机通话的时间．
如图1，在△ABC中，∠ACB=2∠B，∠BAC的平分线AO交BC于点D，点H为AO上一动点，过点H作直线l⊥AO于H，分别交直线AB、AC、BC于点N、E、M．
（1）当直线l经过点C时（如图2），证明：BN=CD；
（2）当M是BC中点时，写出CE和CD之间的等量关系，并加以证明；
（3）请直接写出BN、CE、CD之间的等量关系．
如图1，在一个7×7的正方形ABCD网格中，实线将它分割成5块，再把这5块拼成如精英家教网图2，中间会出现一个小孔，如果正方形ABCD的边长为a，试计算图2中小孔的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网