题目内容
【题目】如图,在△ABC中,∠BAC=20°,∠ABC=30°.
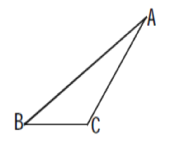
(1)画出BC边上的高AD和角平分线AE;
(2)求∠EAD的度数.
【答案】(1)见解析;(2)50°
【解析】
从三角形的一个顶点向它的对边作一条垂线,画出的这条线段就是三角形的高,注意钝角三角形较短边上的高在三角形的外部,再结合尺规作角平分线的方法即可解答第(1)问;
(2)根据已知条件,在△ABD中运用三角形内角和定理可得到∠BAD的度数,然后由角平分线的定义可得∠BAE=10°,再结合∠EAD=∠BAD-∠BAE即可得到答案.
(1)如图所示,AD为BC边上的高,AE为角平分线.
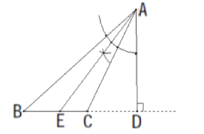
(2)∵AD⊥BD,
∴∠ADB=90°.
∵在△ABD中,∠ADB=90°,∠B=30°,
∴∠BAD=180°-90°-30°=60°.
∵∠BAC=20°,AE为∠BAC的平分线,
∴∠BAE=10°.
∵∠BAD=60°,∠BAE=10°,
∴∠EAD=∠BAD-∠BAE=60°-10°=50°.

练习册系列答案
相关题目