题目内容
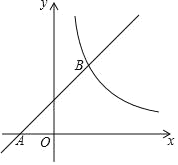
【题目】如图,在平面直角坐标系xOy中,一次函数y=x+b的图象经过点A(﹣2,0),与反比例函数y=![]() (x>0)的图象交于B(a,4).
(x>0)的图象交于B(a,4).
(1)求一次函数和反比例函数的表达式;
(2)设M(m﹣2,m)是直线AB上一点,过M作MN∥x轴,交反比例函数y=![]() (x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
(x>0)的图象于点N,若AONM为顶点的四边形为平行四边形,求点M的坐标.
【答案】(1)y=x+2,![]() ;(2)点M的坐标为
;(2)点M的坐标为![]() .
.
【解析】
(1)用待定系数法求解;(2)由题意可知M(m﹣2,m),点N(![]() ,m),当MN∥AO且MN=AO=2时,四边形AONM是平行四边形,则
,m),当MN∥AO且MN=AO=2时,四边形AONM是平行四边形,则![]() ﹣(m﹣2)=±2,求解即可.
﹣(m﹣2)=±2,求解即可.
解:(1)∵一次函数y=x+b的图象经过点A(﹣2,0),
∴0=﹣2+b,得b=2,
∴一次函数的解析式为y=x+2,
∵一次函数的解析式为y=x+2与反比例函数y=![]() (x>0)的图象交于B(a,4),
(x>0)的图象交于B(a,4),
∴4=a+2,得a=2,
∴4=![]() ,得k=8,
,得k=8,
即反比例函数解析式为:y=![]() (x>0);
(x>0);
(2)∵点A(﹣2,0),
∴OA=2,
由题意可知M(m﹣2,m),点N(![]() ,m),
,m),
当MN∥AO且MN=AO=2时,四边形AONM是平行四边形,
![]() ﹣(m﹣2)=±2
﹣(m﹣2)=±2
解得,m=2 ![]() ,或m=2
,或m=2 ![]() +2(舍弃)(负值已舍去)
+2(舍弃)(负值已舍去)
∴点M的坐标为![]() .
.

【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).