题目内容
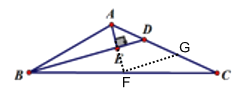
【题目】如图,在△ABC中,BC=2AB,BD为∠ABC的角平分线,∠ADB=45°,过点A作AE⊥BD于点E,若BE=![]() ,则DE的长为__________
,则DE的长为__________

【答案】![]()
【解析】
延长AE交BC于F,过点F作FG∥BD交AC于G,利用ASA易证△ABE≌△FBE,可得AE=EF,AB=BF,进而得到FG是△BDC的中位线,DE是△AFG的中位线,然后根据中位线的性质列方程求解即可.
解:如图,延长AE交BC于F,过点F作FG∥BD交AC于G,
∵BD为∠ABC的角平分线,AE⊥BD,
∴∠ABE=∠FBE,∠AEB=∠FEB=90°,
又∵BE=BE,
∴△ABE≌△FBE(ASA),
∴AE=EF,AB=BF,
∴BC=2AB=2BF,E为AF中点,
∴F为BC中点,
∵FG∥BD,
∴FG是△BDC的中位线,DE是△AFG的中位线,
∴FG=2DE,FG=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目