Question

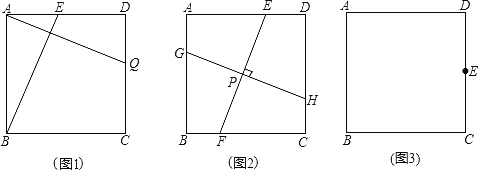
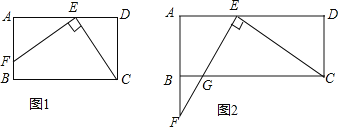
【题目】在矩形ABCD中，已知AD＞AB．在边AD上取点E，使AE＝AB，连结CE，过点E作EF⊥CE，与边AB或其延长线交于点F．

（1）如图1，当点F在边AB上时，线段AF与DE的大小关系为　 　．

（2）如图2，当点F在边AB的延长线上时，EF与边BC交于点G．判断线段AF与DE的大小关系，并加以证明．

（3）如图2，若AB＝2，AD＝5，求线段BG的长．

Answer 1

【答案】（1）AF＝DE；（2）AF＝DE；证明见解析；（3）

【解析】

1）根据题意证明△AEF≌△DCE即可解答；

（2）证明方法与（1）相同可以证明结论；

（3）根据平行线分线段成比例定理列出比例式，计算得到答案．

（1）AF＝DE；

理由是：如图1，∵四边形ABCD是矩形，

∴∠A＝∠D＝90°，AB＝CD，

∵AE＝AB，

∴AE＝CD，

∵EF⊥CE，

∴∠FEC＝∠AEF+∠CED＝∠CED+∠ECD＝90°，

∴∠AEF＝∠ECD，

在△AEF和△DCE中，

，

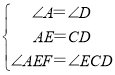∴△AEF≌△DCE（ASA），

∴AF＝DE；

故答案为：AF＝DE；

（2）AF＝DE，

证明：如图2，∵∠A＝∠FEC＝∠D＝90°，

∴∠AEF＝∠DCE，

在△AEF和△DCE中，

，

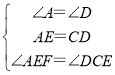∴△AEF≌△DCE（ASA），

∴AF＝DE．

（3）∵△AEF≌△DCE，

∴AE＝CD＝AB＝2，AF＝DE＝3，FB＝FA﹣AB＝1，

∵BG∥AD，

∴，即

∴BG＝．